Seja
Considere a função definida por
e a integral dupla
a) Faça um esboço apurado da região e, ao lado, esboce seu interior.
b) Expresse como um integral iterada, integrando primeiro com respeito a e depois a . Não é preciso calcular a integral!
c) Expresse como integral iterada, integrando primeiro com respeito a e depois a . Não é preciso calcular a integral!
d) Calcule .
e) Determine, usando igualdades e desigualdades, uma região espacial cuja projeção no plano é e cujo volume é igual ao valor de .
Passo 1
a) Partiu esboçar essa região ! Vamos olhar para a primeira desigualdade:
Ela nos diz que está entre a parábola e , certo? Então, desenhemos essa curva e a reta !
Para a parábola, temos algo assim:
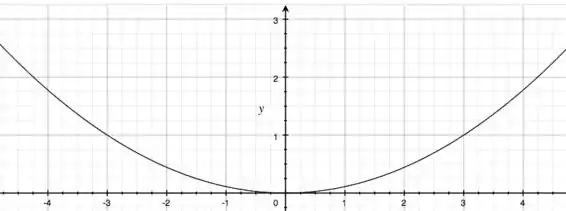
Sabemos que ela tem a boa virada para cima, pois o coeficiente de é positivo. Além disso, ela é bem aberta, pois esse coeficiente é menor que ;)
Para a reta , temos:
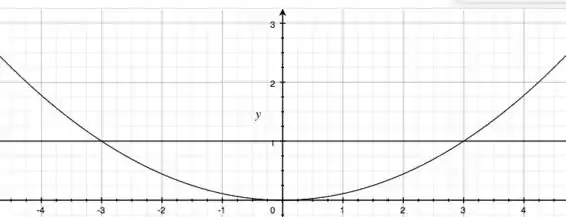
Show? Aqui, temos que prestar atenção no seguinte: colocando na equação da parábola, quais são os valores de ?
Portanto, a reta e a parábola se cruzam em e ! Marque isso no seu gráfico!
Passo 2
Beleza, e agora? Ainda temos a segunda desigualdade! Ela é:
Ou seja, considerando a primeira desigualdade (curvas que desenhamos no passo anterior), temos que limitar nosso entre e ! Assim, teremos apenas a parte do gráfico:
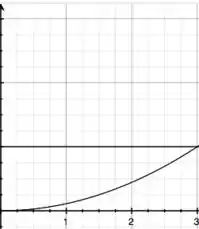
Veja que colocaram a região terminando exatamente no ponto de encontro da reta e da parábola ;)
Show! Agora sabemos tudo o que precisamos, e é só preencher a figura! Como, pela primeira desigualdade sabemos que está acima da parábola e embaixo da reta, é:
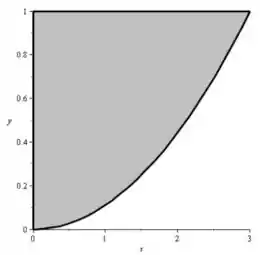
E, para o interior, basta jogar uma linha pontilhada no contorno:
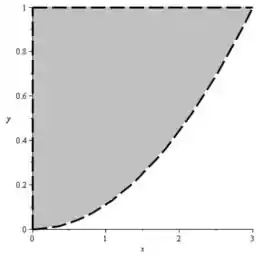
Na realidade, quando o cara pede “o interior de ”, ele quer exatamente a mesma coisa, mas nas desigualdades, em vez de sinais de , temos apenas , sacou?
Passo 3
b) Adoro quando aparece no enunciado “não calcule a integral” XD Vamos lá, é só colocar os limites da região nos limites de integração! Como queremos integrar primeiro em relação a , então o vem antes do . Como é função de , então essa já é a ordem natural de integração! Lembre: numa integral iterada, a integral de dentro fica com a variável que está entre duas funções, e a de fora fica entre constantes!
Enfim, teremos:
Beleza?
Passo 4
c) Agora, precisamos mudar a ordem de integração, primeiro a e depois a . Mas é função de ! Não é o que está entre constantes? Pois, então, vamos fazer virar função de ! Para isso, devemos observar a região de integração “invertendo os eixos”:
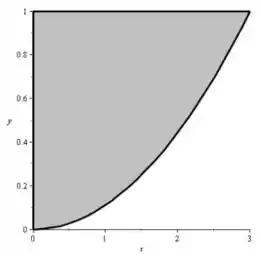
Agora, em vez de pensar quem está entre a parábola e , que é o que vemos com a cabeça em pé, vamos fazer virar função de , e então, teremos:
Agora, estamos na mesma figura, mas com a cabeça virada para a direita! Então, está entre e a parábola , e está entre e ! Acho que facilita ver que é o próprio eixo , e é o eixo !
Agora podemos escreve a integral com esses limites que encontramos:
Passo 5
d) Ok, agora temos que resolver essa integral. Qual das duas ordens de integração será a melhor? Bem, vejamos a primeira:
Nesse caso, teríamos que encontrar a primitiva de . Honestamente, assim, de cara, eu não tenho nenhuma ideia XD Mas... vendo a segunda opção,
Não temos no integrando! E, assim, já temos algum progresso logo de cara, o que parece bom :D Prosseguindo nessa integral, teremos:
Viu? Como não tínhamos nenhum foi simples de integrar! Agora, colocando esses limites par ao ,
Agora, podemos fazer uma substituição simples, colocando , e, então, .
Para os novos limites de integração, temos que, quando , , e, quando , !
Teremos:
Passo 6
e) Esse volume é a integral dupla de uma função sobre o domínio , certo? Se estamos falando de volume, a função que devemos integrar é , ou seja, estamos integrando, em uma área , segmentos cujo comprimento é a “diferença de alturas” das funções.
Como o enunciado disse que o volume é a própria integral que resolvemos, então , pois integramos apenas a ! Assim, sabemos que , e os limites para o e para o permanecem iguais ao do . Nossa região é dada por:
Resposta
a) 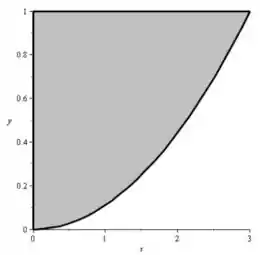
b)
c)
d)
e)