Considere o sólido limitado pela superfície e pelos planos , , , e . Determine o volume do sólido descrito.
Passo 1
Bem, se um problema nos pede volume, o que ele quer verificar se sabemos fazer é calcular essa integral dupla aqui:
Logo, a nossa tarefa principal é determinar quem é , e . Depois é só correr para o abraço e resolver a integral ! Vem comigo então!
Passo 2
Vamos começar determinando a região de integração :
Pelo próprio enunciado, a região de integração é a região no plano . Nesse caso, o problema nos delimitou a região assim:
Colocando cada uma dessas retas no plano a gente logo vê a nossa querida região :
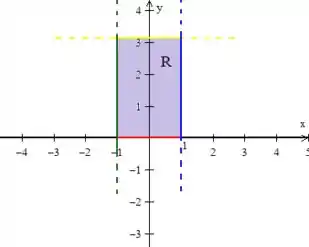
Veja que podemos descrever essa região retangular considerando variando de até :
Enquanto o ...
Passo 3
Quanto à função e a função
A função essa é sempre a função que a gente considera a função que tem um gráfico mais acima. Enquanto isso, a é sempre a função mais abaixo.
O nosso problema nos definiu duas funções:
E
Como é sempre positivo, assim como é positivo, também, considerando o intervalo dado (de a ), a gente conclui que é sempre maior que dentro da região considerada. Logo, a função que está por cima é:
Enquanto que quem está por baixo...
Passo 4
Voltando para a integral e juntando tudo...
Agora é só calcular a integral mesmo. Integrando a de dentro em (e considerando como constante)...
Substituindo os limites em , afinal foi ele quem a gente integrou, ganhamos...
Integrando em ...