UFPE, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº Ricardo F. da Silva - Undécima Lista, Questão 4a
Determine o volume do sólido dado.
a) Abaixo do plano e acima da região limitada por e .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular o volume abaixo do plano e acima da região entre as curvas e . Pra isso, a gente precisa saber que o volume de um sólido qualquer limitado por uma superfície e por um plano é definido através da integral dupla:
Em que é a região limitada no plano , no nosso caso, a região entre as curvas e , e é dado por . Assim, vamos encontrar o intervalo onde varia, igualando as equações das duas curvas. Com isso, definimos nossos intervalos de integração e calculamos a integral dupla do volume.
Vamos lá!
Passo 2
Vamos começar esboçando nossa região:
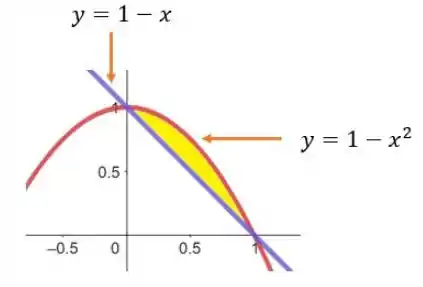
As duas curvas se interseptam quando , assim:
Assim, temos ou . Então, nossos limites laterais são:
E nossos limites em sãos as próprias curvas:
Passo 3
Montando nossa integral, temos:
Observe que a função foi obtida ao isolarmos a variável da equação do plano.
Assim, integrando em relação a , temos:
Aplicando os intervalos de integração em :
Integrando em relação a :
Aplicando os limites de integração em , temos nosso volume:
Valeu, galera! Até a próxima! 😉