Integrais duplas sobre regiões gerais, Coordenadas Polares
Seja a região plana
a)
- Determine a região em coordenadas polares, usando desigualdades, no seguinte formato:
- Determine a fronteira da região em coordenadas polares, usando igualdades e desigualdades.
- Escreva o volume na forma de uma integral dupla iterada nas coordendas polares e .
- Calcule o volume .
explicitando as funções e e as constantes e .
b) Determine as coordenadas radiais dos pontos de fronteira de para e . Em seguida, marque os pontos no desenho abaixo e esboce .
c) Considere a região espacial
Passo 1
a) Desigualdades feia né? Mas, façamos o que o enunciado pede: vamos tacar e , pois estamos em coordenadas polares!
Reescrevendo as variáveis,
Como ,
Sabemos que , então,
Cortando os , temos:
Finalmente, como sabemos que o raio é uma dimensão sempre positiva, e que, pela relação acima não é maior que , então:
Passo 2
Bom, já temos os limites para o raio. E o , de quanto a quanto ele varia? Para isso, podemos olhar para a segunda e terceira desigualdades!
Colocando em coordenadas polares,
E então, como é sempre , temos que e devem ser maiores do que simultaneamente! Isso só ocorre quando :D
Nossa região, por fim, é definida como:
E, para sua fronteira, temos que manter o fixo em seu valor máximo, e percorrer o contorno de , dado por:
Viu? É a mesma coisa, só que em vez de , temos um ;)
Passo 3
b) Vamos lá, agora é trabalho braçal! Para ver os pontos da fronteira de , pegamos a equação , substituímos cada pedido e vemos o valor para o raio.
Para , temos:
Para , temos:
Para , temos:
Para , temos:
Para , temos:
Passo 4
Agora, precisamos juntar os pontos
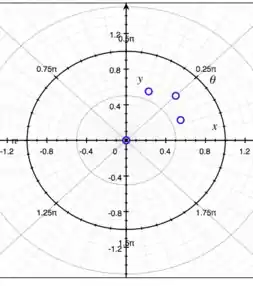
E agora a gente usa da nossa malandragem. Sabemos que senos e cossenos tem sempre a ver com coisas curvas. Então, para esboçar o contorno de , vamos traçar uma curva que passe por esses pontos :D É algo parecido com uma gota:
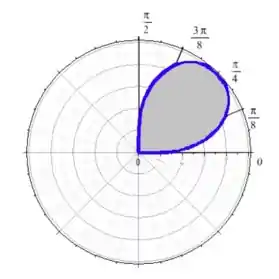
Passo 5
c) Estamos quase lá! Segura mais essa questão! Veja, temos uma região , dada por:
Sabemos que as três últimas desigualdades dizem respeito à região , certo? A única coisa nova que apareceu foi esse , que nada mais é do que a função que estamos integrando! Essa desigualdade nos diz que devemos integrar a função ao longo da região !
Como sabemos, dos passos anteriores, que é definida com entre duas contantes, e e é funçnao de , nossa integral, com o jacobiano, fica:
Lembrando que, em coordenadas polares ;)
Passo 6
Vamos agora resolver essa integral? Primeiro, passemos esse para fora da raiz:
Integrando em relação a , teremos:
Colocando os limites para o ,
Mas, lembra da relação que usamos lá no início, ? Então, o que temos aqui é:
Agora, usando que , teremos:
E, agora sim, podemos encontrar a primitiva, que é:
Ufa! Finalmente, taí o volume!
Resposta
a) ;
b)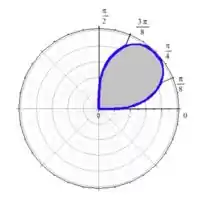 
c) e