UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 9b.
9 - Calcule o volume dos sólidos delimitados pelas superfícies dadas:
b) , e
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nessa questão, temos que calcular o volume de um solido formado pelas equações , e .
Podemos calcular o volume de um sólido através de uma integral dupla onde nossa função de integração é dada pela variação da altura, ou seja, a variação de .
Se desenhássemos essas equações para visualizar nosso sólido, obtemos
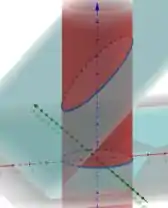
Podemos perceber que os limites da base do nosso solido é circular, então temos que usar coordenadas polares para resolver esse probleminha.
Com isso, para esse caso, a integral é obtida como
Bora começar nossos cálculos? 😁
Passo 2
Primeiro, vamos definir nossa função de integração. Vemos que dois dos nossos limites são e , essa variação de é justamente a nossa função. Ou seja
Convertendo nossa função para polar, substituímos por e por , lembra disso? Então
O que nos resta é obter os valores para e .
E aí? Como fazemos?
Esses valores são nossos valores da base, concorda? O volume de um solido é área da base multiplicado pela altura. A altura já calculamos quando fizemos e obtemos a nossa função de integração.
Com isso, se observarmos nosso solido, vemos que sua base é descrita pela equação . Ou seja, uma circunferência de raio .
Por se tratar de uma circunferência completa, os limites de vai de a e por englobarmos toda a sua parte interna, nosso raio varia de a .
Ou seja
Entendeu? 👀
Passo 3
Dessa forma, nossa integral vai ter a seguinte cara
Primeiro integramos com relação a pelo método de integração de polinômios onde dividimos a variável pela sua potência e somamos no seu expoente.
Aplicando os limites de integração, temos
Agora com base nesse resultado, integramos com relação a
Temos uma constante, onde sabemos que a integral de uma constante é a própria integral multiplicado pela constante de integração. Também temos um que pelo teorema fundamental do cálculo, a integral do é igual ao .
Aplicando os limites de integração, temos
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
