UM circuito elétrico composto por um resistor (de resistência ), um indutor (de indutância ) e uma bateria (com diferença de potencial entre os seus terminais) está ilustrado abaixo.
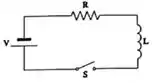
A chave est inicialmente aberta e, consequentemente, não há corrente elétrica passando pelo circuito. No instante , essa chave é ligada e a corrente que atravessa o circuito é solução da seguinte equação diferencial:
Onde são constantes positivas. A expressão que define a corrente , para um instante qualquer, é:
Passo 1
A primeira coisa que temos que observar é que ele deu uma condição inicial ali no texto.
Repara que ele diz que a chave estava fechada, assim que ela for aberta, ou seja, em não terá corrente.
Vamos resolver a nossa EDO
Repara que ela é uma EDO de 1ª ordem linear. Então vamos usar o fator integrante para achar a sua solução, primeiro vamos deixar isolado, para isso vamos dividir a equação toda por
Agora precisamos achar o fator integrante, normalmente o chamamos de , mas essa é a nossa função, então vamos chamar de , só para não nos confundir
Passo 2
Agora, vamos multiplicar o nosso fator integrante pela EDO
A parte da esquerda da equação vai ser
Passo 3
Integrando dos dois lados, vamos ter
Agora, basta isolarmos o , a nossa solução vai ser
Passo 4
Vamos agora usar a nossa condição inicial
A nossa solução vai ser
Podemos colocar em evidência
Resposta
Letra