Considere o problema de valor inicial:
Resolva o problema de valor inicial e esboce as soluções quando:
Passo 1
Fala aí pessoal, tudo bom com vocês?
Nessa questão temos o seguinte problema de valor inicial:
É interessante a gente perceber que não foi dada exatamente a condição inicial, temos ela em função de . Assim precisamos primeiro resolver e EDO em função desse dado, e depois substituímos ele por cada um dos valores dados no enunciado, beleza?
Mas, e como podemos resolver essa equação diferencial? Então, podemos começar verificando se ela é separável. Temos:
Daí:
Excelente! Temos uma equação separável!
Assim, para resolvê-la basta integrar em ambos os lados.
Vem com a gente que vai ficar super claro 😉
Passo 2
Bom, vamos começar integrando a equação separável em ambos os lados:
Começando pela integral da esquerda, temos:
Parece um pouquinho complicado né? Mas, podemos usar um truque nessa fração. Se olharmos direitinho, temos:
Daí, substituindo na integral, temos:
Show!
Resolvendo a integral da direita, temos:
Daí, igualando as duas integrais, e suprimindo uma das constantes, temos:
Podemos reescrever como:
Mas, é apenas uma constante qualquer. Daí:
Logo:
Invertendo os termos:
Logo:
Como:
Podemos escrever:
onde é uma constante real que depende da condição inicial.
Passo 3
Para calcular a constante precisamos substituir a condição inicial:
Temos:
Daí:
Excelente!
Passo 4
Podemos agora finalmente substituir os valores dados para e encontrar as soluções para cada caso:
Puts, esse caso pode parecer problemático já que havíamos encontrado:
E, não podemos dividir por zero.
É que na verdade, para chegar nessa expressão simplifica para , dividimos por durante a solução sem considerar que poderia ser nulo. Assim, vamos voltar um pouco:
Teríamos:
Então, a nossa constante:
Nesse caso a solução em si não faria muito sentido, pois quando separamos a EDO passamos o dividindo.
Temos:
Assim:
O que nos dá o seguinte esboço dessa solução:
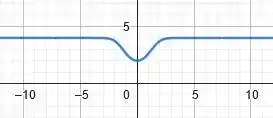
Passo 5
Então, temos:
Assim:
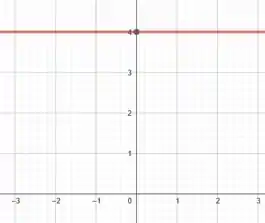
E, por fim:
Logo:
Substituindo:
Cujo esboço:
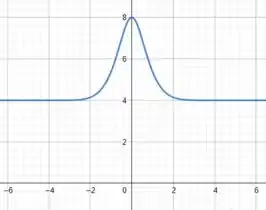
Perfeito galera!
Finalmente matamos esse item. Obrigado pela atenção de todos e até a próxima 😉
Resposta
Resposta no texto.