UFRJ. Cálculo 2. P1. 2022.1. Questão 4.
A solução da equação diferencial , com , e que passa pelo ponto verifica:
(a)
(b)
(c) Nenhuma das opções
(d)
(e) é decrescente em
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nessa questão temos uma EDO de primeira ordem.
Essa questão é bem rapidinha.
A EDO que foi dada no enunciado é dada por
E foi dito que passa pelo ponto , ou seja, temos aqui um problema de valor inicial.
A ideia principal é resolver a EDO e comparar o resultado que encontrarmos com as informações dadas nas alternativas.
Mas como vamos calcular essa EDO? 🤔
Quando temos uma EDO em que podemos separar os termos e em cada lado da equação, aplicamos o método de EDO separável onde depois de dividido, integramos dos dois lados e manipulamos os resultados para isolar .
Entendeu? Veja só!
Passo 2
Podemos escrever a EDO como
Passando tudo que tem de um lado e tudo que tem para o outro lado, temos
Integrando dos dois lados, temos
Passando os dois para um lado só
Por propriedade logarítmica, a soma de é igual a . Logo
Elevando os dois lados pela exponencial
Como é o inverso de e ainda é uma constante, então
Isolando
Pelo método da separação, obtemos a função .
Passo 3
No enunciado, foi dito que deve passar por , dessa forma podemos definir
Substituindo o ponto no resultado que encontramos, temos
Ou seja, nossa função é
Analisando as opções, vemos que a única alternativa correta é a letra (e). podemos provar se plotarmos o gráfico de para
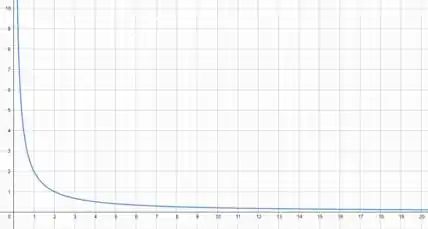
Fim! Iae, o que achou? Responde Aí! 😁
Resposta
(e) é decrescente em