Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Empuxo

Ver Teoria
Exercício 621234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606163646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Física 3 - UFF; P1 de 2019.2

8 - Um bote de madeira tem uma massa de 50 kg. Quando vazio ele flutua na água, com 56% do seu volume submerso. Que massa aproximada de areia pode ser colocada sobre o barco sem que ele afunde? Observe que o barco afundará quando tiver 100% do seu volume submerso.

  1. 22   k g
  2. 15   k g
  3. 89   k g
  4. 73   k g
  5. 46   k g

Passo 1

Ora! Sabemos que a força peso do barquinho vazio é dependente da massa dele M B :

P B = M B g  

Ainda sabemos que se ele está flutuando na água, o que sugere uma força de empuxo apontando para cima. Se você desenhar, vai ganhar algo assim:

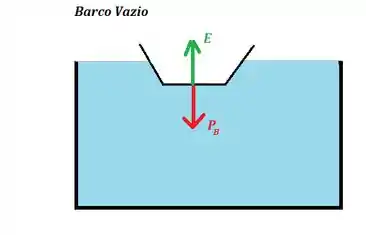
Para o barco não afundar, a força empuxo tem que ser igual à força peso:

P B = E

M B g = E

Como o empuxo é dado por essa equação aqui...

E = ρ A V A g

Então...

M B g = ρ A V A g   →

M B = ρ A V A

Onde V A é o volume de água deslocado pelo barquinho. Em outros termos é o volume submerso do barquinho:

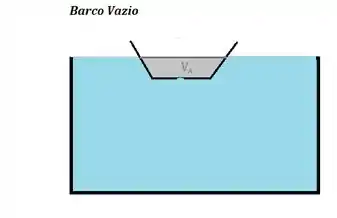
Como o barquinho vazio, ele flutua com 56 % do volume total submerso. Então o volume submerso V A é...

V A = 0,56   V B

Então...

M B = ρ A V A     →

M B = ρ A 0,56 V B

Passo 2

Beleza, essa foi a análise com ele vazio. Se ele estiver cheio de areia ele vai “afundar” até que o volume submerso seja todo o volume do barquinho V B ...

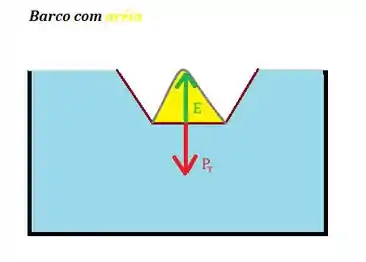
Novamente, embora ele esteja quase afundando, ainda podemos falar que o peso é igual ao empuxo:

P T = E

P T aqui não é o partido não haha. É a informação do peso total do barquinho devido a massa do barco e a massa da areia M a r e i a . Então...

M B + M a r e i a g = ρ A V A g     →

V A é sempre o volume submerso. Nesse caso é todo o volume do barco V B ...

M B + M a r e i a g = ρ A V B g  

M B + M a r e i a = ρ A V B

Passo 3

Então as duas equações que chegamos aos últimos passos foram...

M B = ρ A 0,56 V B               e               M B + M a r e i a = ρ A V B

Dividindo uma pela outra...

M B + M a r e i a M B = ρ A V B ρ A 0,56 V B   →

M B + M a r e i a M B = 1 0,56   →

M B + M a r e i a M B = 1 0,56   →

1 + M a r e i a M B = 1 0,56   →

Isolando a massa da areia...

M a r e i a = M B 1 0,56 - 1

O Bote tem 50   k g ...

M a r e i a = 50 1 0,56 - 1

M a r e i a = 39,28   k g

Passo 4

Se você procurar essa resposta lá, não vai encontrar nada. Isso porque ele quer a opção de massa (ou opções) que o barco não afunde. Se colocarmos 39,28   k g o barco afundará, pois fizemos considerando a menor massa para que o barquinho ficasse 100 % por baixo dágua (tanto é que consideramos no passo dois V A = V B ).

As opções que atendem esse requisito são A e B. Afinal, as outras opções passam de 40   k g .

Resposta

Letra A e B.

Exercícios de Livros Relacionados

Na Fig 14-38, um cubo de aresta L   =   0,600   m e 450   k g de massa é suspenso por uma corda em um tanque aberto que contém um líquido de massa específica 1030   k g / m ³ ³. Determine (a) o módulo
Que fração de volume de um iceberg (massa específica 917k g / m ³ ³) é visível se o iceberg flutua (a) na água salgada (massa específica 1024k g / m ³ ³) e (b)em um rio (água doce, massa específica 10
Um flutuador tem a forma de um cilindro reto,com 0,5m de altura e 4,0m ² ² de área das bases; sua massa específica é 0,4 vezes a massa específica da água doce. Inicialmente o flutuador é mantido total
Que fração de volume de um iceberg (massa específica 917k g / m ³ ³) é visível se o iceberg flutua (a) na água salgada (massa específica 1024k g / m ³ ³) e (b)em um rio (água doce, massa específica 10
Um bloco de madeira flutua em água doce com dois terços do volume V submersos e, em óleo, com 0,90 × V submersos. Determine a massa específica (a) da madeira e (b) do óleo.