Ordene as densidades dos blocos , e .
Passo 1
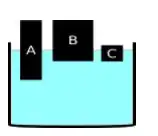
Na teoria de empuxo vimos que quando o corpo está em equilíbrio igual na figura acima. Sendo assim o empuxo equilibra o peso.
Vimos que o empuxo é dado por:
Cortando a aceleração da gravidade. E escrevendo a massa do corpo em função da densidade.
Isolando a densidade do corpo, vemos que ela é proporcional a fração do corpo submersa:
Devido a isso conseguimos relacionar que quanto maior for a fração de volume submerso maior é a densidade do corpo.
E por esta relação conseguimos ver que a fração de volume submerso segue esta ordem na figura:
E por isso
Resposta
Alternativa
Exercícios de Livros Relacionados
Na Fig 14-38, um cubo de aresta L = 0,600 m e 450 k g de massa é suspenso por uma corda em um tanque aberto que contém um líquido de massa específica 1030 k g / m ³ ³. Determine (a) o módulo
Que fração de volume de um iceberg (massa específica 917k g / m ³ ³) é visível se o iceberg flutua (a) na água salgada (massa específica 1024k g / m ³ ³) e (b)em um rio (água doce, massa específica 10
Um flutuador tem a forma de um cilindro reto,com 0,5m de altura e 4,0m ² ² de área das bases; sua massa específica é 0,4 vezes a massa específica da água doce. Inicialmente o flutuador é mantido total
Que fração de volume de um iceberg (massa específica 917k g / m ³ ³) é visível se o iceberg flutua (a) na água salgada (massa específica 1024k g / m ³ ³) e (b)em um rio (água doce, massa específica 10
Um bloco de madeira flutua em água doce com dois terços do volume V submersos e, em óleo, com 0,90 × V submersos. Determine a massa específica (a) da madeira e (b) do óleo.