A figura abaixo apresenta a medição da massa de uma esfera de chumbo em duas situações, utilizando dinamômetro e balança. Sabendo que a esfera metálica com densidade de e volume de , está totalmente submersa em água. Determine as leituras , em quilogramas, para as situações mostradas na figura. Justifique sua resposta.

Só pra começar, vou dizer que mesmo a figura do enunciado não sendo de uma esfera, as de baixo vão ser e isso não muda nada na nossa questão, beleza? Então bora! Concorda comigo que o sistema da direita é meio enrolado? Sólido na água com balança e dinamômetro, muita coisa! Vamos olhar então pra situação da esquerda primeiro:

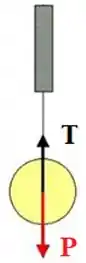
Como o nosso sólido não sobe nem desce quando está suspenso pelo dinamômetro, vemos que há um equilíbrio vertical de forças:

O dinamômetro calcula a tensão e divide ela pela gravidade pra encontrar a massa do objeto que está segurando. De forma geral:

Nesse nosso caso, como e se igualam, então a leitura nada mais é do que:

Olha, a gente pode até não ter a massa da bolinha, maaaas, sabemos que podemos relacionar a massa com a sua densidade da seguinte forma:

E assim, temos tudo pra pegar a leitura , pois do enunciado:

Partiu, como está tudo no mesmo:

Agora, na situação da direita, a coisa muda um pouco. Com a nossa esfera submersa, o empuxo aparece pra “ajudar a levantar a esfera”.

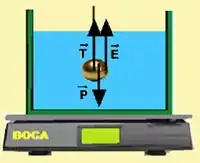
Portanto agora o dinamômetro passa a ler um peso aparente. Como ele lê e o diagrama de forças é:

Da fórmula do peso e do empuxo, temos:

Já que temos que dividir tudo pela gravidade mesmo, a leitura do dinamômetro será:

Como a esfera está completamente submersa, o volume de água deslocada vai ser o mesmo () da esfera, tranquilo? Como é uma constante conhecida, temos tudo pra calcular já! Mãos a obra!

Colocando em evidência e substituindo os valores em seguida, temos:

E daí em diante é terminar as contas:

Agora vamos falar da balança! De novo, vai ser importante olharmos pra todas as forças. Em relação ao passo anterior, a tensão não sumiu nem nada. Nem o peso da esfera ou o empuxo sobre ela:

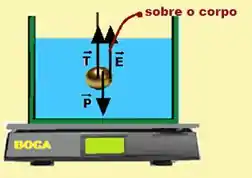
Só que galera, toda ação gera uma reação! Igual em módulo, sentidos opostos, e sobre corpos diferentes. Se a reação do é realizado sobre a Terra e a reação da tração é realizada sobre a corda, kedê a reação do empuxo? Bem, vai estar sobre a água!

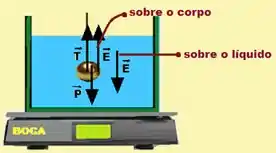
Tem mais uma coisinha pra gente considerar: o peso do sistema copo-água! Como ele vai estar apontando pra baixo também, sabemos agora exatamente quais forças estão envolvidas na leitura da balança:

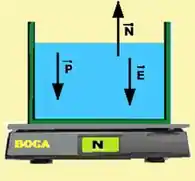
A leitura será então:

E dividindo tudo por :

E tudo isso o enunciado deu, ou então nós já achamos! A massa do copo com a água tava indicada na balança da esquerda na figura do enunciado, e vale nove quilos. Sendo assim: