Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Empuxo

Ver Teoria
Exercício 721234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071737475767778798081828384858687888990919293949596979899100

Enunciado

Uma bola de ferro encontra-se submersa em água, suspensa por uma corda presa a uma prancha de surf (figura abaixo). A prancha tem um volume total de 30 l , massa específica média de 90 k g / m 3 e flutua com 1 / 3 do seu volume submerso.

Faça um diagrama das forças que atuam no sistema e calcule o raio da bola de ferro

Dados:

ρ f e r r o = 7,90 × 10 3   k g / m 3

Passo 1

Quais forças estão nesse sistema? Temos o peso da prancha, o peso da bola, os empuxos de cada um e tração do fio que conecta os dois. Apontando as forças, fica mais ou menos assim:

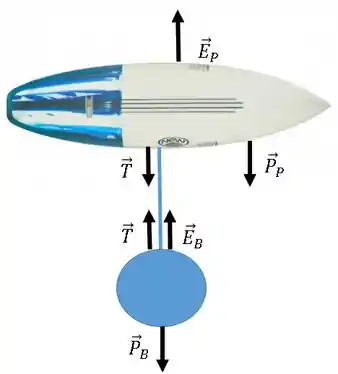
Passo 2

Como foi dado a densidade da bola de ferro, podemos calcular a massa dessa bola e sabendo a massa podemos calcular o volume e depois calcular o raio dela!

Como o sistema está em equilíbrio temos que para a bola

T + E B = P B

Como a bola está completamente afundada, então o empuxo dessa bola é dado por

E B = V B ρ á g u a g

Já o peso dessa bola é dado por

P B = m B g = V B ρ f e r r o g

Onde relacionamos a massa com a densidade por ρ f e r r o = m B / V B

Assim a nossa equação pra bola fica

T + V B ρ á g u a g = V B ρ f e r r o g

T = V B g ρ f e r r o - ρ á g u a

V B = T g ρ f e r r o - ρ á g u a

Só que não temos a tração no fio! Pra achar ela, vamos olhar para a prancha

Passo 3

A condição de equilíbrio da prancha é

E P = T + P P → T = E P - P P

O empuxo na prancha é dado por

E P = V d e s l o c ρ á g u a g

O enunciado diz que 1 / 3 da prancha está submersa, ou seja

V d e s l o c = V P 3 = 30 3 = 10 l

Convertendo para m 3 ( 1 l = 10 - 3 m 3 )

V d e s l o c = 10 × 10 - 3 = 10 - 2 m 3

Assim o empuxo da prancha fica

E P = V d e s l o c ρ á g u a g = 10 - 2 × 10 3 × 10

E P = 100   N

Já o peso da prancha é dado por

P P = m P g = ρ P V P g

Usando os dados do enunciado temos

P P = 90 × 30 × 10 - 3 × 10

P P = 27 N

Assim

T = E P - P P = 1 00 - 27

T = 73   N

Passo 4

Agora podemos calcular o volume da esfera!

V B = T g ρ f e r r o + ρ á g u a = 73 10 7,9 × 10 3 - 10 3

V B = 1,058 × 10 - 3 m 3

Para calcular o raio basta fazer

V B = 4 3 π R 3

R = 3 V B 4 π 1 / 3 = 3 × 1,058 × 10 - 3 4 π 1 / 3

R = 0,0632   m = 6,32   c m

Resposta

R = 0,0632   m = 6,32   c m

Exercícios de Livros Relacionados

Na Fig 14-38, um cubo de aresta L   =   0,600   m e 450   k g de massa é suspenso por uma corda em um tanque aberto que contém um líquido de massa específica 1030   k g / m ³ ³. Determine (a) o módulo
Que fração de volume de um iceberg (massa específica 917k g / m ³ ³) é visível se o iceberg flutua (a) na água salgada (massa específica 1024k g / m ³ ³) e (b)em um rio (água doce, massa específica 10
Um flutuador tem a forma de um cilindro reto,com 0,5m de altura e 4,0m ² ² de área das bases; sua massa específica é 0,4 vezes a massa específica da água doce. Inicialmente o flutuador é mantido total
Que fração de volume de um iceberg (massa específica 917k g / m ³ ³) é visível se o iceberg flutua (a) na água salgada (massa específica 1024k g / m ³ ³) e (b)em um rio (água doce, massa específica 10
Um bloco de madeira flutua em água doce com dois terços do volume V submersos e, em óleo, com 0,90 × V submersos. Determine a massa específica (a) da madeira e (b) do óleo.