A figura abaixo mostra duas bolas de mesmo raio, , imersas num recipiente contendo dois fluidos de densidades diferentes, óleo e água, cujas densidades são e , respectivamente. Estas bolas estão ligadas por um fio fino de massa desprezível. A bola está com metade de seu volume submerso em óleo e a outra metade em ar, e a bola , que é vezes mais densa que a bola , está com metade de seu volume submerso em óleo e a outra metade em água. As respostas deverão ser dadas no Sistema Internacional de unidades.
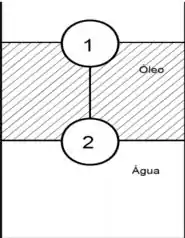
- Desenhe o diagrama de forças que atuam sobre a bola e sobre a bola . Despreze o empuxo do ar presente na parte superior do sistema.
- Encontre as densidades das bolas e ( e ).
- Encontre as massas das bolas e .
- Encontre a tração no fio.
Passo 1
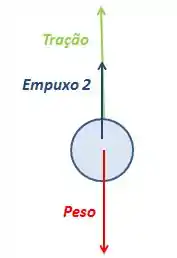
a): Bom, as forças que atuam sobre cada bloco são: A tração, o peso e o empuxo.
Então:
Pra primeira bolinha (1):
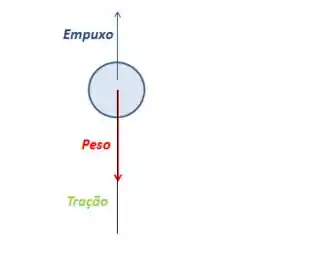
Pra segunda bolinha:
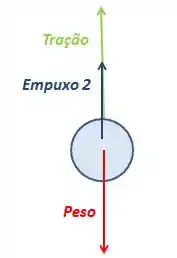
Observação: A segunda bolinha está em contato com dois fluidos: A água e o óleo. Então, o empuxo que ela sofre é a soma dos empuxos dos dois fluidos. Fique atento a isso!
Passo 2
b):
Beleza, agora queremos achar a densidade de cada uma. Pra isso, como o sistema está em equilíbrio, vamos precisar montar a equação de equilíbrio das forças de cada uma:
Pra primeira:
Pra segunda:
Notou? O segundo empuxo vale:
Ok, mas esse sistema ainda tem incógnitas demais. O enunciado nos diz que a segunda bola é 6 vezes mais densa que a primeira. Então, por causa dessa informação, vale a pena reescrever o sistema passando a descrever os pesos com as densidades:
Passo 3
Com isso nosso sistema vira:
Subtraindo a segunda da primeira gente consegue eliminar e fica com
Dá pra cortar esse montão de e !!!
Agora isolando
Vamos converter os valores das densidades para (Basta multiplicar por 1000):
Então:
Como
Passo 4
c):
Tendo as densidades das bolas, é fácil descobrir a massa de cada uma. Podemos calcular o volume das esferas, já que temos o raio. O volume de uma esfera é dado por:
Sendo
Então:
E:
Passo 5
Isolando em alguma das equações, como nessa:
Resposta
a):
Pra primeira bolinha (1):
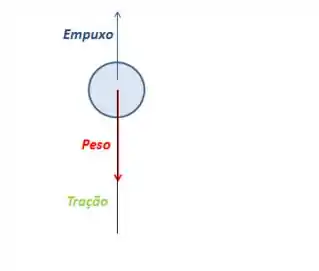
Pra segunda bolinha:
b):
c):
d):