Uma esfera completamente imersa em um líquido de densidade é amarrada ao fundo do recipiente por um barbante. A tensão no barbante corresponde a um quinto do peso da esfera. A densidade da esfera é igual a:
A)
B)
C)
D)
E)
Passo 1
Se pensarmos no diagrama de forças que agem na esfera,
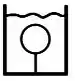
Temos o peso e a tração puxando a esfera para baixo, e o empuxo forçando para cima.
Como o sistema está em equilíbrio
A questão diz que
Passo 2
Temos que o peso é
Se usarmos a densidade da esfera:
Então,
Lembrando que o empuxo é
Usando a equação obtida no passo anterior:
Obtemos que
Resposta
C)
Exercícios de Livros Relacionados
Na Fig 14-38, um cubo de aresta L = 0,600 m e 450 k g de massa é suspenso por uma corda em um tanque aberto que contém um líquido de massa específica 1030 k g / m ³ ³. Determine (a) o módulo
Que fração de volume de um iceberg (massa específica 917k g / m ³ ³) é visível se o iceberg flutua (a) na água salgada (massa específica 1024k g / m ³ ³) e (b)em um rio (água doce, massa específica 10
Um flutuador tem a forma de um cilindro reto,com 0,5m de altura e 4,0m ² ² de área das bases; sua massa específica é 0,4 vezes a massa específica da água doce. Inicialmente o flutuador é mantido total
Que fração de volume de um iceberg (massa específica 917k g / m ³ ³) é visível se o iceberg flutua (a) na água salgada (massa específica 1024k g / m ³ ³) e (b)em um rio (água doce, massa específica 10
Um bloco de madeira flutua em água doce com dois terços do volume V submersos e, em óleo, com 0,90 × V submersos. Determine a massa específica (a) da madeira e (b) do óleo.