Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Empuxo

Ver Teoria
Exercício 411234567891011121314151617181920212223242526272829303132333435363738394042434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

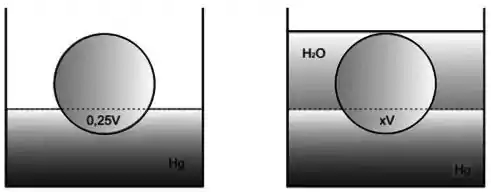
II - Uma esfera homogênea flutua com 25% do volume submerso em mercúrio. Ao ser colocada em um recipiente contendo água e mercúrio, fica completamente submersa, parte do volume em água e parte em mercúrio.

d) Determine a massa específica da esfera. (Volume da esfera V)

e) Determine o percentual do volume submerso em mercúrio nesta nova configuração.

Dados:

p a t m = 1,0113 × 10 5   P a = 1   a t m

g = 10 m / s 2

ρ á g u a = 1,00 × 10 3 k g / m 3

ρ m e r c ú r i o = 13,6 × 10 3 k g / m 3

Passo 1

Aqui, temos sistemas em que o empuxo, para cima, equilibra o peso, para baixo.

P = E

Lembrando que o empuxo pode ser calculado como:

E = ρ l i q g V s u b m e r s o

Passo 2

d) Olhando a imagem da esquerda, temos empuxo causado apenas pelo mercúrio, então:

P e s f e r a = E H g

m e s f e r a g = ρ H g g V s u b m e r s o

Podemos escrever a massa da esfera em função da sua massa específica:

m e s f e r a = ρ e s f e r a V

Substituindo m e s f e r a e V s u b m e r s o = 0,25   V . Obtemos

ρ e s f e r a V g = ρ H g g 0,25 V

ρ e s f e r a = 0,25 ∙ ρ H g = 0,25 ∙ ( 13,6 × 10 3 k g / m 3 )

ρ e s f e r a = 3,4 × 10 3   k g / m 3

Passo 3

e) Porcentagem do volume submerso em mercúrio (x).

Na imagem da direita, temos agora dois empuxos, um do mercúrio e um da água:

P e s f e r a = E H 2 O + E H g

ρ e s f e r a V g = ρ H 2 O g V H 2 O s u b m e r s o   + ρ g V H g s u b m e r s o

Se, segundo a imagem, temos V H g s u b m e r s o = x V , na água teremos

V H 2 O s u b m e r s o   = V - x V = 1 - x V

Substituindo tudo:

ρ e s f e r a V g = ρ H 2 O g 1 - x V + ρ H g g x V

Cortando V e g:

ρ e s f e r a = ρ H 2 O - x ρ H 2 O + ρ H g x

x = ρ e s f e r a - ρ H 2 0 ρ H g - ρ H 2 O = 3,4 × 10 4 - 1,0 × 10 4 13,6 × 10 4 - 1,0 × 10 4

x = 0,19 = 19 %

Resposta

d) ρ e s f e r a = 3,4 × 10 3   k g / m 3  

e) x = 19 %

Exercícios de Livros Relacionados

Na Fig 14-38, um cubo de aresta L   =   0,600   m e 450   k g de massa é suspenso por uma corda em um tanque aberto que contém um líquido de massa específica 1030   k g / m ³ ³. Determine (a) o módulo
Que fração de volume de um iceberg (massa específica 917k g / m ³ ³) é visível se o iceberg flutua (a) na água salgada (massa específica 1024k g / m ³ ³) e (b)em um rio (água doce, massa específica 10
Um flutuador tem a forma de um cilindro reto,com 0,5m de altura e 4,0m ² ² de área das bases; sua massa específica é 0,4 vezes a massa específica da água doce. Inicialmente o flutuador é mantido total
Que fração de volume de um iceberg (massa específica 917k g / m ³ ³) é visível se o iceberg flutua (a) na água salgada (massa específica 1024k g / m ³ ³) e (b)em um rio (água doce, massa específica 10
Um bloco de madeira flutua em água doce com dois terços do volume V submersos e, em óleo, com 0,90 × V submersos. Determine a massa específica (a) da madeira e (b) do óleo.