O prisma maciço da figura abaixo com altura , comprimento , largura , e massa é um modelo simples de um navio com carga padrão. Na água (densidade ), a parte submersa tem altura . Considere , e . Para atracar em portos de interesse, esse navio deve ter .
- Qual deve ser a porcentagem (?
- Neste caso, quanto vale a pressão no fundo do navio em atmosferas?
(Dados: )
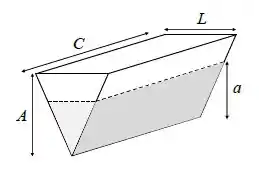
Passo 1
Bom pessoal, para que possamos atracar o nosso navio temos que o empuxo exercido pelo volume de água deslocado tem q ser igual ao peso do navio, logo:
O enunciado nos diz que a parte submersa do navio deve ter altura , por semelhança de triângulos temos que:
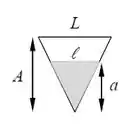
Então:
Substituindo o comprimento na fórmula, temos:
Passo 2
Definindo a razão como , chegamos a:
Ou seja;
.
Passo 3
A pressão no fundo do navio é dada pela soma da pressão atmosférica mais a pressão exercida pela coluna d’água.
Resposta
a) 50
b) 2 atm
Exercícios de Livros Relacionados
Na Fig 14-38, um cubo de aresta L = 0,600 m e 450 k g de massa é suspenso por uma corda em um tanque aberto que contém um líquido de massa específica 1030 k g / m ³ ³. Determine (a) o módulo
Que fração de volume de um iceberg (massa específica 917k g / m ³ ³) é visível se o iceberg flutua (a) na água salgada (massa específica 1024k g / m ³ ³) e (b)em um rio (água doce, massa específica 10
Um flutuador tem a forma de um cilindro reto,com 0,5m de altura e 4,0m ² ² de área das bases; sua massa específica é 0,4 vezes a massa específica da água doce. Inicialmente o flutuador é mantido total
Que fração de volume de um iceberg (massa específica 917k g / m ³ ³) é visível se o iceberg flutua (a) na água salgada (massa específica 1024k g / m ³ ³) e (b)em um rio (água doce, massa específica 10
Um bloco de madeira flutua em água doce com dois terços do volume V submersos e, em óleo, com 0,90 × V submersos. Determine a massa específica (a) da madeira e (b) do óleo.