Um béquer com água tem massa total de e está em repouso sobre um prato de balança. Um bloco de alumínio de , suspenso por um dinamômetro, é totalmente mergulhado na água do béquer, como mostra a figura ao lado. (massa específica do alumínio: , massa específica da água: )
c) Determine a leitura do dinamômetro, calibrado em
d) Determine a leitura da balança, em

Passo 1
c):
Bom, galera, aqui a gente vai precisar montar a equação que rege todas as forças que agem sobre o bloco. As forças são: o peso, o empuxo e a tensão (que é o que o dinamômetro mede).
É isso! Achando a tensão, acharemos a resposta.
Primeiro temos que apontar as forças. Tanto o empuxo quanto a tensão apontam pra cima, enquanto o peso pra baixo.
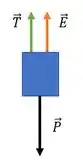
Como o bloco está em equilíbrio, a soma das forças dará zero:
Então a nossa tensão fica
Vamos calcular essas duas forças!
O peso é fácil, pois o enunciado já nos deu a massa:
Passo 2
O Empuxo é dado por:
Mas não sabemos . No entanto, temos a densidade do alumínio e a sua massa. Assim, fica fácil encontrar o volume por ele deslocado:
Ok! Então voltando para a tensão
E finalmente
Beleza! Essa é a calibração do dinamômetro!
Passo 3
d):
A balança mede a Normal, certo? E qual Normal? É a Normal entre o bequer com água e a balança. Como o béquer está em equilíbrio basta apontar as forças nele.
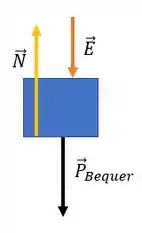
Ué?!?!?!?! Empuxo apontando para baixo?! Pode isso, Arnaldo?!
A regra é clara! Se tem um empuxo sobre o bloco de alumínio produzido pela água no béquer, pela terceira lei de Newton, tem que ter uma força de reação com mesma intensidade, só que no sentido oposto!
Ah tá! Então esse empuxo pra baixo é a reação do bloco sobre o liquido! Beleza, então! Segue jogo!
Então usando a condição de equilíbrio
E finalmente!
Isso aí!
Resposta
c):
d):