Uma bola de plástico de raio igual a flutua em repouso na água com de seu volume submerso.
- Que força você precisa aplicar à bola para mantê-la em repouso completamente abaixo da superfície da água?
- Se você soltar a bola, qual vai ser a aceleração dela no instante em que a soltar?
Dica: Volume de uma esfera de raio :
Dados:
Densidade da água:
Gravidade:
Passo 1
a)
Bom, temos aqui um problema que envolve três forças. Quais são elas?
O Peso, o Empuxo e a Força externa.
Abaixo podemos ver um esquema dessas três forças atuando no corpo( A força azul é o peso, a verde o empuxo e a vermelha a força externa):
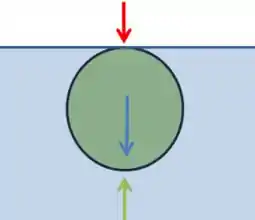
Opa, mas essa é a formação final do sistema, certo?
E no início? Bem, no início o corpo estava apenas flutuando na água com de seu volume submerso. Isso é, havia apenas o empuxo e o peso no início:
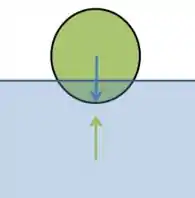
Passo 2
Bom, vamos ter que analisar a situação inicial antes de partir pra luta. Por que? Porque precisamos saber o valor do peso da bola pra calcular a força que devemos aplicar.
No início, só havia o peso e o empuxo. A bola estava em equilíbrio, flutuando, o que nos leva a:
O empuxo inicial é o empuxo causado por do volume do corpo, ou seja:
Notou ali em cima o fator multiplicando o volume? Justamente, porque tem apenas do volume abaixo da água. Assim:
Passo 3
Agora podemos calcular a força que devemos aplicar quando todo o volume está submerso.
Quando todo o volume está submerso, o empuxo é máximo e vale:
Então, olhando a direção de cada força na figura que vimos no primeiro passo, teremos o seguinte somatório de forças( que precisa ser nulo de novo, já que o corpo está novamente em repouso):
E essa é a resposta da letra a).(:
Passo 4
b):
Agora imagine que você retire a força que dava equilíbrio pro sistema. Vamos ter uma força resultante diferente de zero e que vai gerar uma aceleração, certo?
Essa força é dada por:
Mas não sabemos a massa da bola, certo?
Bom, mas sabemos o peso. Ai fica fácil:
Assim, a aceleração será:
Uma bela aceleração, não é mesmo?
Resposta
a):
b):