Um bloco de madeira cúbico com aresta de flutua sobre uma interface entre uma camada de água e uma camada de óleo, com sua base situada abaixo da superfície livre do óleo. A densidade do óleo é igual a ³ e a da água
- Qual é a pressão manométrica na face superior do bloco?
- Qual a pressão manométrica na face inferior do bloco?
- Quais são a massa e a densidade do bloco?
Passo 1
a):
Bom, como sabemos a distância da superfície livre do óleo até a face superior do bloco, sabemos a altura da coluna de fluido acima dele. Assim:
Assim:
Passo 2
b):
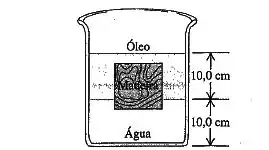
Olhando a nossa figura, podemos ver que a camada de óleo tem
E a camada de água?
Ela tem , já que o cubo afundou em relação à superfície do óleo (como diz o enunciado).
Assim, a pressão na face inferior vai ser a soma das pressões causadas pela coluna de óleo e pela coluna de água:
Passo 3
Como o corpo está em equilíbrio, podemos dizer que:
E esse empuxo seria:
Você pode estar pensando: Bora calcular cada um desses empuxos!
Porém, existe uma forma mais fácil: Lembra que o empuxo é a força causada pela diferença de pressão entre as faces superior e inferior? Pois bem, podemos dizer que:
Sendo que a área da face do cubo vale:
Assim:
Assim:
E a densidade? Bom, já temos a massa, só calcular o volume e aplicar a fórmula.
Assim:
Resposta
a):
b):
c):