Um bloco cúbico com densidade e aresta de comprimento flutua sobre um líquido de densidade maior .
a) Qual fração do volume do bloco fica acima da superfície do líquido.
b) O líquido é mais denso do que a água (densidade igual a ) e não se mistura com ela. Derramando-se água sobre a superfície do líquido, qual deve ser a camada da água para que a superfície livre da água coincida com a superfície superior do bloco? Expressa a resposta em termos de , , e . Calcule a profundidade da camada da água de parte (b) se o líquido for mercúrio e o bloco for de aço com aresta de 10,0 cm.
Dados:
Passo 1
a):
Vamos escrever as expressões pro peso e pro empuxo:
E pro peso:
Como o bloco está em equilíbrio, podemos igualar as forças:
Pronto, essa é a fração do volume que fica submerso. Pra descobrir qual é a fração que fica acima da superfície livre, basta subtrair isso do 1:
Passo 2
b):
Bom, nessa nova situação vão existir dois empuxos: Um causado pela água e um causado pelo fluido. Além disso, a configuração espacial do problema vai ficar assim:
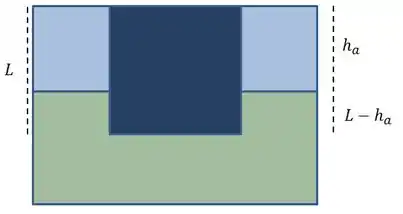
Como você pode ver, a camada de água, o que queremos descobrir, é representada por . A camada de água coincide com a superfície do bloco.
Assim, o volume submerso na água será dado por:
E o volume submerso no fluido vai ser dado por vezes a área:
Passo 3
Show? Como esse novo sistema também está em equilíbrio, podemos dizer que a soma dos empuxos será igual ao peso:
Lembrando que:
Cortando nos dois lados:
Como e , o denominador e o numerador vão ser negativos, então vamos multiplicar ambos por
Calculando para o aço e o mercúrio:
Resposta
a):
b):