A figura abaixo ilustra um cubo de aresta e massa , totalmente imerso em um fluido de densidade constante . O cubo é suspenso por um fio inextensível, como mostrado na figura. No local, a aceleração da gravidade é constante e igual a , e aponta para baixo (na direção paralela ao fio), enquanto a pressão do ambiente é a pressão atmosférica, que também é constante e igual a . Nestas condições, calcule:
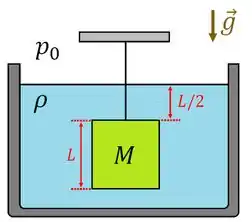
(a) O módulo da força de empuxo a que o cubo está submetido.
(b) O módulo da força de tensão no fio.
(c) A pressão na face inferior do cubo.
Passo 1
Letra : Primeiramente, vamos lembrar o que é o empuxo. O empuxo (denotado por ) é a força que aparece em um corpo submerso devido ao fluido em que está submerso. O empuxo é a resultante das forças que aparecem no corpo devido à diferença de pressão que atua nas diferentes partes do corpo em questão.
O módulo do empuxo pode ser calculado a partir da seguinte expressão
sendo a densidade do fluido no qual o corpo está submerso, é o volume de fluido que foi deslocado pelo corpo e o módulo da aceleração da gravidade, suposta constante. O produto é igual a massa do volume de fluido deslocado pelo corpo. Assim, podemos ver o empuxo como o peso do volume deslocado (em módulo). É importante lembrar que o empuxo sempre está direcionado para cima!!
Para o nosso caso, o volume deslocado é igual ao volume do cubo, pois ele está totalmente submerso. Deste modo,
Portanto, o módulo do empuxo é dado por
Vamos para o próximo item!
Passo 2
Letra : Para saber o módulo da tensão, devemos analisar as forças sobre o cubo. Desta forma, considere abaixo o diagrama de corpo livre do cubo.
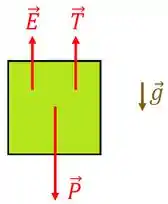
Da figura acima, como o cubo está em repouso, temos que
Sabemos que e, do item anterior, . Portanto,
Passo 3
Letra : Para responder este item, utilizaremos a lei de Stevin. Esta lei nos diz que a pressão de um ponto no fluido que está a uma altura da superfície é dada por
sendo a pressão atmosférica. A altura é a profundidade (a partir da superfície do líquido) do ponto no qual se deseja calcular a pressão.
Desta forma, considere novamente a figura do enunciado.
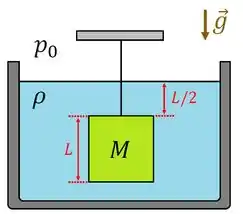
Assim, pela figura, vemos que a face inferior do cubo está a uma altura
Portanto, temos finalmente que