Um bloco maciço de volume e densidade é mantido submerso num líquido de densidade uniforme por meio de um cabo (vide a figura abaixo). É dado o módulo da aceleração gravitacional . Observação: e são os vetores unitários na horizontal e vertical, conforme indicado na figura. Resposta aos itens abaixo, em função dos dados:
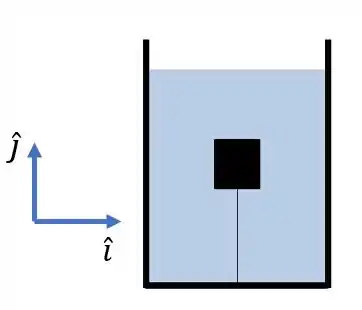
- Suponha neste item que o recipiente contém liquido e o bloco esteja em repouso em um referencial inercial.
- Qual o empuxo que o liquido faz sobre o bloco?
- Determine a tensão que o cabo exerce sobre o bloco a partir da 2ª Lei de Newton.
- Deduza o empuxo que o líquido faz sobre o bloco, explicando o cálculo da diferença de pressão entre as superfícies inferior e superior do objeto e aplicando a 2ª Lei de Newton
- Obtenha a tensão que o cabo exerce sobre o bloco a parti da 2ª Lei de Newton em termos dos dados e dos módulos de , e
Passo 1
a)
a1)
O empuxo vai ser dado por:
a2)
Pela segunda lei de Newton, vamos ter:
Onde o empuxo nós já sabemos e o peso vai ser:
A força resultante vai ser dada por:
Como ele está em repouso, a força resultante é nula:
Passo 2
b)
b1)
O empuxo é o resultado entre a diferença de pressão em cima e embaixo do bloco.
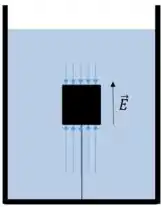
Podemos ver o empuxo como a soma entre a força que a pressão abaixo do bloco faz e a força que a pressão acima do bloco faz.
A primeira tem sentido para cima e a segunda sentido para baixo.
Logo:
Vamos supor que a altura do bloco é e a área da sua seção é e que ele está a uma profundidade .
A pressão em cima é:
A pressão na parte mais baixa vai ser:
Vamos ter:
O volume do corpo é:
Passo 3
b2)
Já vimos que:
Dessa vez a força resultante vai ser:
Substituindo os valores na equação das forças, vamos encontrar:
Lembrando, do item a, que:
O módulo de é:
Logo: