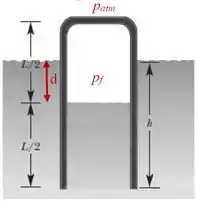
Um cano de comprimento aberto em uma das extremidades, contém ar à pressão atmosférica. O cano é introduzido verticalmente em um lago de água doce até que a água atinja metade da altura do tubo. Suponha temperaturas iguais para a água e para o ar em todo o processo.
- Determine a pressão do ar preso dentro do tubo.
- Determine a profundidade, , da extremidade inferior do tubo.
- Sabendo que o cano flutua nessa posição e a área da seção reta é de , determine a massa do cano.
Dados:
Passo 1
Para um gás ideal temos que
Temos uma compressão isotérmica e pela figura vemos que o volume foi reduzido a metade.
Temos que antes da compressão o gás dentro do cano tem pressão , volume e temperatura e depois da compressão tem pressão , volume e temperatura . Assim
Passo 2
Igualando a pressão da coluna de água de altura e a pressão na interface gás/água dentro do cano temos
Pela figura podemos relacionar o comprimento do cano e a distância
Passo 3
O que mantém o cano flutuando é a força de empuxo! A força de empuxo é dada por
Como o cano está em equilíbrio, temos que o peso do cano é igual ao empuxo
Agora precisamos calcular o volume deslocado. O volume deslocado vai ser a coluna de altura e base com área (atenção que !!!). Então temos
E agora podemos calcular a massa do cano
Resposta
(a)
(b)
(c)