Duas bolinhas, uma de isopor e outra metálica são ligadas por um fio ideal. Suas massas são tais que ao serem imersas em um líquido de densidade , ficam em perfeito equilíbrio, com o fio tensionado, e sem tender nem a flutuar nem a afundar. Se imergimos as bolinhas num outro líquido com , podemos afirmar que:

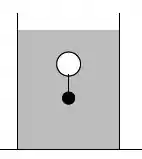
(a) As bolas tenderão a afundar

(b) As bolas tenderão a flutuar

(c) As bolas continuarão mantendo o equilíbrio

(d) Nada podemos afirmar sem saber os valores das massas e de e

Se você tivesse só um objeto sozinho que nem flutuasse e nem afundasse, totalmente dentro de um fluido com densidade , poderíamos relacionar o empuxo com o peso desse objeto por

Se agora nós colocássemos este mesmo objeto totalmente afundado num fluido com densidade a força resultante sobre esse objeto seria

Onde definimos como positivo a direção para cima e como negativo a direção para baixo.

Como já relacionamos com

Como , e o objeto afundará!