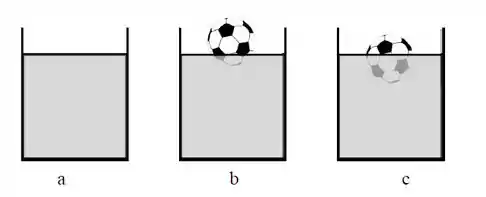
A figura abaixo mostra três recipientes iguais, preenchidos pelo mesmo fluido incompressível até a mesma altura. Em dois deles bolas estão flutuando. Marque a resposta que ordena corretamente os recipientes de acordo com o peso total P (recipiente + fluido + bola):
Passo 1
Essa é uma questão que testa o seu conhecimento sobre empuxo.
Quando temos um corpo flutuando em um fluido, quanto vale a massa do volume deslocado pelo fluido?
Vale exatamente o peso do corpo. Sabemos isso pela equação:
Passo 2
Bom, pelas figuras, os níveis dos fluidos são iguais. Isso quer dizer que houve um deslocamento de fluido nas figuras 2 e 3.
A questão é: No que isso afeta o peso total?
A resposta é: Nada.
Como vimos, a massa de fluido na figura 2 e 3 será igual a massa do corpo que está flutuando. Dessa forma, nada muda, porque o fluido deslocado é compensado pela massa adicionada.
Assim:
Resposta
e)