Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Empuxo

Ver Teoria
Exercício 651234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636466676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Empuxo

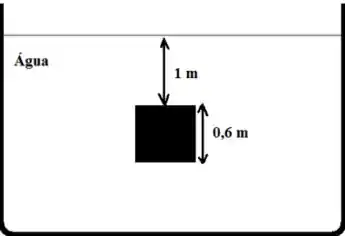
Na figura, um cubo de aresta L = 0,600 m e 100 k g de massa é mantido submerso, com a face superior a uma profundidade de 1,00 m , num tanque aberto que contém água ρ = 10 3 k g / m 3

Na superfície do tanque a pressão é atmosférica. ( 1,013 x 10 5 P a ) .

g = 9,8   m / s 2

  1. Calcule o valor da pressão manométrica e da pressão absoluta na face inferior do cubo.
  2. Suponha que o cubo seja liberado a partir da profundida descrita acima. Determine a força resultante sobre o cubo imediatamente após a liberação.
  3. Desprezando as forças de atrito viscoso, calcule o tempo que demora a face superior para atingir a superfície do tanque.
  4. Depois de algum tempo, observa-se que o cubo flutua com uma das faces paralela à superfície da água. Calcule a altura da parte submersa do cubo.

Passo 1

a):

Bom galera, antes de mais nada, vamos lembrar que pressão absoluta é a pressão total em determinado local, ou seja, a pressão da coluna de líquido mais a pressão atmosférica, enquanto a pressão manométrica é apenas a pressão da coluna de líquido.

Podemos dizer também que a pressão manométrica é igual a pressão absoluta menos a pressão atmosférica.

Beleza, nessa questão fica mais fácil primeiro calcular a pressão manométrica e depois somar a ela o valor da pressão atmosférica pra achar a pressão absoluta.

O enunciado pede pra gente calcular a pressão logo abaixo do cubo. Pelo princípio de steven, essa pressão é a mesma pra todos os pontos com essa profundidade...então podemos calcular a pressão logo do lado do cubo, de acordo com a coluna de líquido que existe ali:

p m = ρ g H

Onde H é:

H = 1 + 0,6 = 1,6 m

Então:

p m = ρ g H = 10 3 . 9,8 . 1,6 = 1,56 x 10 4   P a

Agora basta a gente somar isso à pressão atmosférica:

p a b s = p m + p a t m = 1,013 x 10 5 + 0,156 x 10 5 = 1,169 x 10 5 P a

Passo 2

b):

Quais são as forças que agem no cubo? Bom, são a força peso e o empuxo.

Vamos calcular cada uma. A força peso é dada por:

P = m g = 100 . 9,8 = 980   N

E o empuxo é dado por:

E = ρ g V

Onde V é o volume de líquido deslocado. Como todo o corpo está submerso, o volume deslocado é igual ao volume do cubo:

V = 0,6 3 = 0,216   m 3

Então:

E = 10 3 . 9,8 . 0,216 = 2116,8   N

Como o empuxo é maior que o peso, sabemos que a resultante apontará pra cima:

F R = E - P = 2116,8 - 980 = 1136,8   ≅ 1,14 x 10 3 N

Passo 3

c):

Aqui nós temos um exercício simples de cinemática. Vamos primeiro descobrir qual é a aceleração do bloco usando a segunda lei de Newton e a força resultante:

F R = m a R → a R = F R m = 1,14 x 10 3 100 = 11,4   m / s 2

Ótimo! Agora vamos usar aquela formulinha de Física 1( Qualquer dúvida, dê uma olhada lá no nosso guia de Física 1):

∆ S = 1 2 a t 2

Nós sabemos o ∆ S e a aceleração, precisamos descobrir o tempo.

O ∆ S é a distância da face superior do cubo até a superfície do líquido e é:

∆ S = 1   m

Então:

1 = 1 2 . 11,4 . t 2 → 2 11,4 = t 2 → t = 2 11,4 ≅ 0,42   s

Passo 4

d):

Isso acontece depois que o cubo já atingiu a superfície do líquido e passa a ficar uma pouco para fora.

Precisamos descobrir qual o volume submerso que equilibra o peso, porque assim não há resultante de força e ,logo, o bloco fica estático:

E = P

E = ρ g V s u b → ρ g V s u b = m g

∴

V s u b = m g ρ g = m ρ = 100 10 3 = 0,1

Sendo a área da seção do cubo dada por:

A = 0,6 2 = 0,36

Precisamos descobrir a altura tal que:

A h = V s u b = 0,1

Então:

0,36 . h = 0,1 → h = 0,1 0,36 ≅ 0,28   m

Resposta

a):

p m = 1,56 x 10 4   P a

p a b s = 1,169 x 10 5 P a

b):

F R   ≅ 1,14 x 10 3 N

c):

t ≅ 0,42   s

d):

h ≅ 0,28   m

Exercícios de Livros Relacionados

Na Fig 14-38, um cubo de aresta L   =   0,600   m e 450   k g de massa é suspenso por uma corda em um tanque aberto que contém um líquido de massa específica 1030   k g / m ³ ³. Determine (a) o módulo
Que fração de volume de um iceberg (massa específica 917k g / m ³ ³) é visível se o iceberg flutua (a) na água salgada (massa específica 1024k g / m ³ ³) e (b)em um rio (água doce, massa específica 10
Um flutuador tem a forma de um cilindro reto,com 0,5m de altura e 4,0m ² ² de área das bases; sua massa específica é 0,4 vezes a massa específica da água doce. Inicialmente o flutuador é mantido total
Que fração de volume de um iceberg (massa específica 917k g / m ³ ³) é visível se o iceberg flutua (a) na água salgada (massa específica 1024k g / m ³ ³) e (b)em um rio (água doce, massa específica 10
Um bloco de madeira flutua em água doce com dois terços do volume V submersos e, em óleo, com 0,90 × V submersos. Determine a massa específica (a) da madeira e (b) do óleo.