- Um balão de Hélio, sob condições normais, ergue uma cesta e uma carga com massa( cesta + carga + material do que é feito o balão) de . Nessas condições, a massa específica do ar é de e a do Hélio é de .
- Desenhe o diagrama de forças e calcule qual deve ser o volume mínimo do balão de Hélio para erguer a cesta com carga.
- Suponha que o balão de ar esteja com o volume calculado no item a. Se a carga ( for removida, calcule o módulo da aceleração na nova situação.
Passo 1
a):
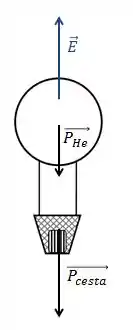
Passo 2
Então galera, quais são as forças que agem no balão? Bem, temos o peso total do balão, que é a soma do peso do gás() com o peso da cesta( .
Pra descobrir o volume mínimo que o balão precisa ter pra se sustentar no ar, basta a gente montar a equação de equilíbrio do sistema, isso é:
Sendo que o empuxo é dado por:
E o peso do balão é dado por:
E esse ai é o tal do volume que queremos achar!
E o peso da cesta é a massa da cesta vezes a gravidade:
Então:
Passo 3
b):
Pra gente achar a aceleração, a gente precisa achar a força Resultante.
Removendo-se uma massa da massa total do balão, nós vamos diminuir o peso que o puxa pra baixo, e isso vai fazer com que a força resultante tenha a mesma direção que o empuxo que está para cima.
Logo:
Sendo a massa original:
Ou seja, a massa da cesta mais a massa do Hélio, a nova massa vai ser essa massa menos a massa que retiramos:
Sacou?
Então, vamos calcular essa força resultante:
E a aceleração anda mais é do que:
Resposta
a):
b):