Considere as figuras abaixo. Nas questões abaixo explique claramente o seu raciocínio.
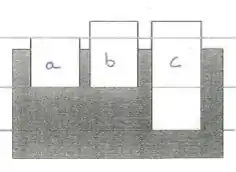
Ordene em sequência decrescente as densidades dos blocos e .
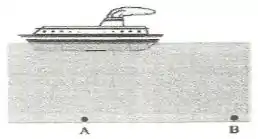
na figura abaixo. A pressão no ponto é maior ou igual a pressão no ponto ?
Passo 1
Na teoria de empuxo vimos que quando o corpo está em equilíbrio igual na figura acima. Sendo assim o empuxo equilibra o peso.
Vimos que o empuxo é dado por:
Cortando a aceleração da gravidade. E escrevendo a massa do corpo em função da densidade.
Isolando a densidade do corpo, vemos que ela é proporcional a fração do corpo submersa:
Devido a isso conseguimos relacionar que quanto maior for à fração de volume submerso maior é a densidade do corpo.
E por esta relação conseguimos ver que a fração de volume submerso segue esta ordem na figura:
A fração submersa de é a menor. Porém a fração de e são bem próximas, depois de um debate entre a galera daqui chegamos em consenso que a fração submersa de é maior que a de , mas como são próximas você pode não concordar e dizer que são iguais, bem, deixe isso claro e desenvolva a resposta de acordo com o que escolheu.
Se você acha que são iguais então sua resposta deve ser:
E por isso
Mas se você concorda comigo e acha que a fração submersa de é um pouquinho maior que a de a resposta é:
E por isso
Passo 2
O princípio de Stevin diz que em um mesmo fluido dois pontos a mesma altura irão ter a mesma pressão.
Então pelo princípio de Stevin os pontos e possuem a mesma pressão. Não importa se o no ponto tem um navio ou uma bola, isso por que o peso do navio vai ser compensado pelo empuxo da água sobre ele!
Resposta