Três blocos de mesmo tamanho e com massas indicadas abaixo, estão suspensos por balanças enquanto são mergulhados num fluido, conforme a figura ao lado. Seja o peso aparente aquele indicado pela balança nesta configuração. Como se ordenam os pesos aparentes dos blocos?
Dados: e (Obs: Assuma que os fios são inextensíveis, de massa desprezível. Note que o fio do bloco B é naturalmente maior que os outros)
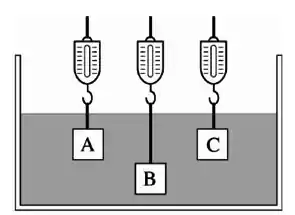
Passo 1
Vamos lá! A questão busca testar o nosso conhecimento sobre três forças muito importantes; Peso , empuxo e tensão no fio .
O empuxo é uma força que contrabalanceia o peso de um objeto, que está parcial ou totalmente submerso em um fluído. E é por causa dessa força que os objetos flutuam em um determinado fluído, nos dando a sensação do peso ser mais leve do que ele realmente é. A isso damos o nome de peso aparente!
Bom, como o enunciado não nos dá nenhuma informação sobre aceleração do bloco, vamos considerar que o bloco está em repouso e com aceleração nula, podemos então escrever o somatório das forças no bloco de acordo com a seguinte equação:
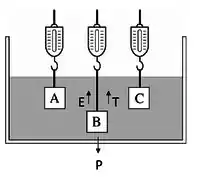
Passo 2
A forma de resolver essa questão é através do equilíbrio de forças, e busca-se descobrir o peso aparente do bloco, sendo este, o valor medido por um tipo de balança chamada dinamômetro. Portanto, rearranjando a equação descrita acima, temos que:
Sendo: a densidade do fluido e o volume do bloco (já que está totalmente submerso).
A massa do bloco pode ser definida como Sendo a densidade do bloco.
Passo 3
Como todos os blocos têm o mesmo volume, conclui-se que:
- O peso aparente só depende das densidades;
- A relação entre as densidades é igual a relação entre as massas;
Logo a relação entre os pesos aparentes também fica igual a relação entre as massas. Portanto, como o enunciado nos diz que e .
Logo:
Resposta
Letra D.