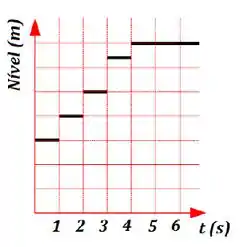
Suponha que quatro bolas maciças feitas de diferentes materiais são jogadas em um recipiente cilíndrico com óleo, uma de cada vez, nos instantes t = 1s, t = 2s, t = 3s e t = 4s. O gráfico ao lado descreve o nível (altura) da superfície do óleo em função do tempo. Sabendo que as bolas lançadas em t = 1s e t = 4s afundaram, ao passo que a segunda e a terceira bola flutuaram, marque a afirmação errada.

(a) O empuxo na primeira bola é igual ao empuxo na segunda bola.

(b) A segunda bola tem um volume maior que o da primeira.

(c) A densidade da terceira bola é menor que a do óleo.

(d) A densidade da quarta bola é maior que a do óleo.

(e) A quarta bola é mais densa que a segunda bola.

(f) A terceira bola tem volume maior que a segunda bola.

Vamos lembrar da fórmula do empuxo:

Repare que vai ser constante, só o que vai mudar é h (o nível do líquido que sobe).

Vamos analisar alternativa por alternativa.

a) O nível subiu igual pra primeira e pra segunda esfera. Então o empuxo vai ser igual mesmo! Tá certo.

b) O empuxo vai ser igual nas duas esferas! Isso quer dizer que as duas deslocaram o mesmo volume. Mas a primeira afundou e a segunda flutuou, né? Então a que tá flutuando ainda tem um volumezinho que tá pra fora do líquido, não submerso. Ou seja, o volume da segunda é maior. Ta certo!

c) Tá certo ! Porque a bola flutua.

d) Também tá certo! Porque a bola afunda.

e) Tá certo ! Porque a quarta bola afunda, a segunda não. Então a densidade é maior na quarta.

f) Como a variação do nível de líquido foi maior na terceira que na segunda bola, podemos escrever:

As duas flutuaram, então o peso é igual ao empuxo pra cada uma. Então:

Como , podemos escrever:

Mas , então:

Como nós não sabemos a densidade, não podemos afirmar mais nada sobre o volume. Então tá errada! Eita!