Um bloco cúbico homogêneo de aresta flutua em repouso na interface entre dois fluidos incompressíveis de densidades e , como mostra a figura abaixo. Considere o módulo da aceleração da gravidade igual a (suposto constante).
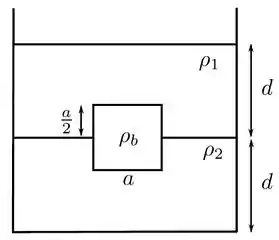
Calcule o empuxo que o bloco sofre.
Calcule a densidade do bloco .
Passo 1
Letra : Primeiramente, vamos lembrar o que é o empuxo.
O empuxo (denotado por ) é a força que aparece em um corpo submerso devido ao fluido em que está submerso. O empuxo é a resultante das forças que aparecem no corpo devido à diferença de pressão que atua nas diferentes partes do corpo em questão.
Assim, para resolver este item, devemos calcular a resultante das forças empregadas pelos fluidos.
ATENÇÃO!! Note que não estamos calculando todas as forças sobre o cubo (ainda falta a força peso). O empuxo é a resultante somente devido ao fluido.
Passo 2
Para o nosso caso, as forças que atuam sobre o cubo são horizontais (força nas paredes laterais) e verticais (forças na parte superior e inferior). Veja a figura.
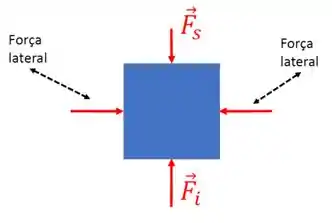
Como o bloco está flutuando, podemos considerá-lo em repouso. Assim, as forças laterais se cancelam e podemos dizer que o empuxo é dado pela diferença entre a força que atua na parte inferior e a força que atua na parte superior , isto é,
pois e estão na mesma direção. Como veremos, devido a pressão nas partes superior e inferior. Agora precisamos calcular os módulos das forças e .
Passo 3
O módulo da força que atua na parte superior do cubo é dado por
sendo a pressão na parte superior do cubo, isto é, a pressão a profundidade de da superfície. Veja a figura.
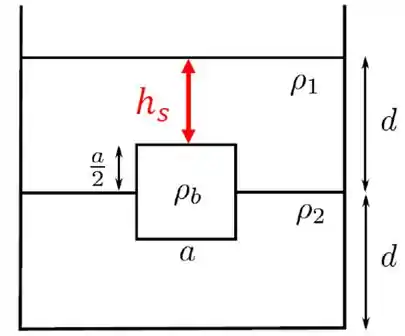
Podemos determinar a partir da lei de Stevin. Assim,
com a pressão atmosférica.
Assim, temos que
Vamos calcular agora . Sabemos que é dada por
sendo a pressão na parte inferior do cubo, isto é, a pressão a profundidade de da superfície. Veja a figura.
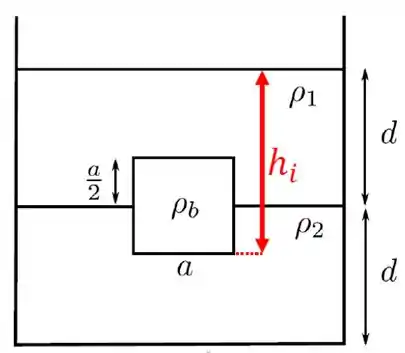
Podemos determinar a partir da lei de Stevin. Assim,
Note que a pressão tem contribuição dos dois fluidos.
Assim, temos que
Portanto, o módulo do empuxo é dado por
Passo 4
Letra : Para calcular a densidade do cubo, utilizaremos o fato do mesmo estar flutuando. Como o cubo está em repouso, então a resultante de TODAS as forças sobre ele (lembre que as forças laterais se anulam) é
sendo a força peso sobre o cubo.
Passo 5
Sabemos que cubo é homogêneo. Assim, sua massa se relaciona com sua densidade por
Logo,