Um copo de água contendo um cubo de gelo a 0°C está cheio até a borda. Uma parte do cubo de gelo sobressai da superfície.

À medida que o gelo derrete, você observa que

 o nível de água permanece inalterado. 

 a água transborda.   a água transborda dependendo da quantidade de massa do cubo de gelo.   o nível de água diminiu.   não dá pra saber sem o conhecimento da pressão atmosférica.

A o gelo tem uma densidade um pouco menos que a da água, o que o enunciado evidencia quando fala que o gelo sobressai da superfície da água, pois como tem densidade menor ele, não afunda.

Bem, vamos esquecer a parte do gelo que sobressai por um tempinho, vamos pegar só o volume de gelo que está na linha D’água

Imagina que essa parte do volume possui massa , e ocupa um volume , então a densidade é dada por

Como a densidade da água é maior que a do gelo, então é preciso de um volume menor para a mesma massa, certo?

Então,

Então falta um volume de água ali, que será preenchido pelo gelo acima da água que tínhamos, lembra??

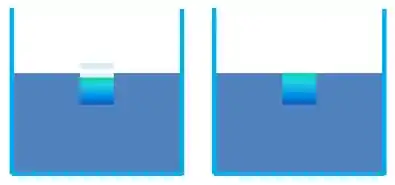
Isso é mágica??? A exata quantidade de gelo para fora da água irá preencher o exato volume de água que falta para á linha d`água continuar a mesma??

Nâo é mágica, meu caro Watson, é física! O que acontece é que como a densidade é inversamente proporcional ao volume, significa que se a razão das densidades for X, nesse caso, essa será a razão de volume submerso, por isso o que sobressai da água, quando se liquefaz, garante que a linha d’água não varie.