Uma esfera metálica oca flutua quase totalmente submersa em água. Sendo as densidades da água e do ferro, respectivamente, e , a razão entre os volumes interno e externo da esfera vale:
(a) 2/10
(b) 1/8
(c) 7/8
(d) 8/7
Passo 1
Primeiramente, vamos lembrar o que é o empuxo. O empuxo (denotado por ) é a força que aparece em um corpo submerso devido ao fluido em que está submerso. O empuxo é a resultante das forças que aparecem no corpo devido à diferença de pressão que atua nas diferentes partes do corpo em questão.
O módulo do empuxo pode ser calculado a partir da seguinte expressão
sendo a densidade do fluido no qual o corpo está submerso, é o volume de fluido que foi deslocado pelo corpo e a aceleração da gravidade, suposta constante. O produto é igual a massa do volume de fluido deslocado pelo corpo. Assim, podemos ver o empuxo como o peso do volume deslocado (em módulo). É importante lembrar que o empuxo sempre está direcionado para cima!! Vamos para o próximo passo.
Passo 2
Primeiramente, vamos analisar o diagrama de forças da nossa esfera oca. O mesmo é dado na figura abaixo.
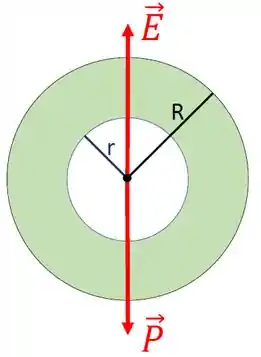
Na figura anterior, é a força empuxo sobre a esfera submersa e é a força peso da esfera. Como a esfera está praticamente submersa e parada no fluido, podemos dizer que a resultante das forças que atuam sobre a esfera é nula. Deste modo, temos que
E agora, no próximo passo, analisaremos cada uma dessas forças.
Passo 3
Para o nosso caso, o módulo do empuxo sobre a esfera pode ser calculado por
O volume de fluido deslocado pela esfera corresponde ao volume externo da esfera, isto é, . Assim, temo que
Vamos guardar essa equação. Considere agora o módulo da força Peso. Sabemos que o mesmo é dado por
sendo a massa da esfera.
A massa da esfera pode ser expressa da seguinte forma
com a densidade da esfera e o volume da esfera. Como a esfera é feita de ferro, então . Temos também que, como a esfera é oca, então o volume da esfera é dado por
sendo o volume da parte externa da esfera oca (ou o volume da esfera de raio ) e o volume da parte oca da esfera (ou o volume da esfera de raio ).
Deste modo, podemos escrever o módulo da força peso da esfera como
Assim, vamos todas as peças que encontramos para resolver o problema no próximo passo.
Passo 4
Agora temos todos os ingredientes para resolver o problema. Vamos nessa!Mostramos no passo 2 que
E no passo 3 que
Juntando tudo, temos que
O enunciado diz que e . Logo,
Portanto, a razão é igual a .
Passo 5
Analisando todas as alternativas, vemos que a alternativa correta é a letra .