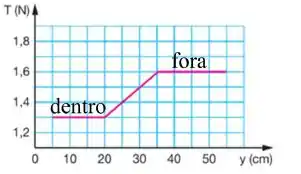
Um cilindro com 15 cm de altura e 2,5 cm² de área de secção transversal, imerso totalmente num líquido, é puxado lentamente para cima, com velocidade constante, por meio de um fio, até emergir do líquido. O gráfico da força de tração T no fio em função da distância , medida a partir do fundo do recipiente até a base do cilindro. São desprezíveis a força devida à tensão superficial do líquido e o empuxo exercido pelo ar sobre o cilindro.
Considerando a altura do nível do líquido independente do movimento do cilindro, e a aceleração da gravidade igual a 10 m/s², determina a massa específica (densidade) do líquido, em .
- 700 kg/m³
- 800 kg/m³
- 900 kg/m³
- 1000 kg/m³
- 1100 kg/m³
Passo 1
E aí, galerinha! Tudo na paz por aí?
Po, esse problema tá falando direto pra gente sobre empuxo, então provavelmente esse negócio vai ser importante por aqui. E como é mesmo a fórmula pro empuxo?
Eitaaaaa, olha ali a densidade do fluido aparecendo que é o que a gente quer. Mas tá, e como a gente vai encontrar esse paranauê dos outros parâmetros. Bem, vamos desenhar primeiro nosso problema.
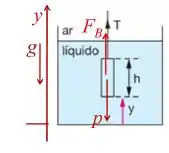
Onde no diagrama de corpo livre é a força de empuxo, P é a força peso e T é a tração que é dada no gráfico, beleza?
Opaaaaa, olha que maravilha então, a gente consegue fazer um balanço de forças quando o cilindro estiver dentro e fora do líquido, certo?
Já captou o que a gente vai precisar fazer? Senão foi ainda, fica tranquilo e VEM COMIGOOOOO!
Passo 2
Fora do líquido a gente sabe pelo gráfico que as únicas forças que vão atuar no cilindro é peso e tração, certo?
Ou seja, já sabemos o valor do peso do cilindro!!!!
Passo 3
E quando estamos dentro do fluido com o cilindro, o gráfico diz pra gente que a força de tração vale 1,3 N.
O balanço de forças quando estiver submerso diz que:
Vamos isolar
Mas que V é esse? É o volume deslocado pelo cilindro quando ele está submerso no fluido. Esse volume deslocado quando todo o cilindro estiver submerso deve ser igual ao volume do próprio cilindro.
Esse A é a área de secção transervsal do cilindro que foi dada em cm²! Bora transformar isso em m² e h é a altura do cilindro que deve ser convertida em m.
Logo
Passo 4
Substituindo os valores:
See you na próxima questão heinnn!!
Resposta
(B)