Quando uma coroa de massa é submersa em água, uma balança acurada registra uma massa de (ver figura). A tabela abaixo mostra as massas específicas de vários metais.
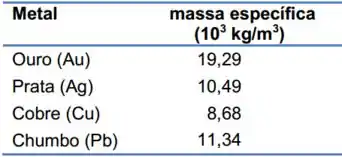
- Em cada caso da figura, faça um diagrama de forças que atuam-na coroa.
- Calcule a massa específica média da coroa e verifique se ela é de ouro maciço.
- Caso a coroa tenha sido confeccionada em prata com banho de ouro, calcule a razão entre as massas de ouro e de prata e obtenha a porcentagem de ouro na coroa.
Passo 1
a):
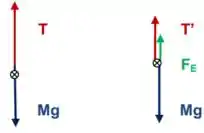
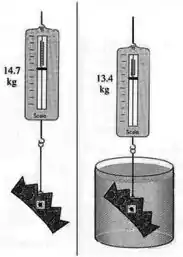
Como você pode ver, na primeira figura não há empuxo, já que não há fluido. Assim, a tensão na corda é maior. Já na segunda a tensão é menor me módulo porque existe o empuxo.
Passo 2
b):
Bom galera, a massa específica da coroa é calculada por:
Sendo que a primeira figura nos dá a massa da coroa, né? Ela vale:
Beleza. Precisamos descobrir o volume. Como faremos?
Vamos usar o empuxo, já que a é a única coisa que muda no sistema da segunda figura. Na segunda figura, a segunda lei de Newton nos dá:
E o peso a gente sabe calcular facilmente por:
A tensão é dada pela massa da balança vezes a gravidade:
Então:
Então, usando a fórmula do empuxo:
Então :
Não é ouro maciço!
Passo 3
c):
Bom galera, o caminho pra resolver isso é meio trabalhoso, mas é fácil de se entender. Vamos lá
A massa específica pode ser escrita como:
Ou seja, é a massa de ouro mais a massa de prata divididas pelos volumes de prata mais o volume de ouro.
Que também pode escrita como:
Já que a massa dividida pela sua massa específica nos dá o volume.
Show!Essa vai ser nossa primeira equação. Nossa segunda equação será:
É a massa total da coroa.
Então temos o sistema( já colocando os valores):
Resolvendo esse sistema:
Então o percentual de ouro na prata é:
E o percentual de ouro em relação à massa total é:
Resposta
a):
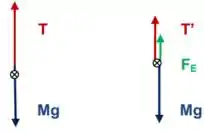
b):
c):