Um bloco maciço de volume V e densidade é mantido submerso num líquido de densidade uniforme () por meio de um cabo (vide a figura abaixo). É dado o módulo da aceleração gravitacional g.
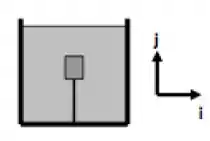
Observação: e são os vetores unitários na horizontal e vertical, conforme indicado na figura. Supondo que o recipiente está em repouso em um referencial inercial, o empuxo que o líquido exerce sobre o bloco e a tensão que o cabo exerce sobre o bloco são dados, respectivamente por:
(a) e
(b) e
(c) e
(d) e
(e) e
Passo 1
Quais são as forças atuando no bloco? Peso, tração e empuxo.E como elas se relacionam?
Isso porque o corpo tá parado, então a força resultante deve ser zero. Beleza?
Passo 2
Maravilha! Vamos escreveras fórmulas dessas forças:
E vamos trocar:
Como o vetor gravidade aponta pra baixo:
Então:
Resposta
Letra E.