Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
UFU, Sem Campus, Cálculo 2, Listas de C2 - Profª Ana Paula - Lista 7 - Integrais Duplas, Questão 8a
Calcular a área das seguintes regiões :
- delimitada pelas curvas e .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para calcular a área da região delimitada pelas curvas e .
Em outras palavras, queremos a seguinte região:
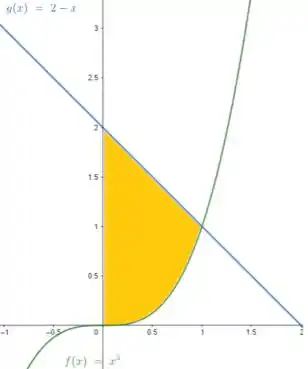
Pelo esboço acima, podemos concluir que a região é dada por:
Obs: o limite de integração foi encontrado igualando e.
Eaí? Bora lá?
😉
Passo 2
Assim, resolvendo a integral, encontramos:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Esboce a região de integração e mude a ordem de integração. ∫ 0 1 ∫ a r c t gx π / 4 f x , yd yd x
Calcule a integral trocando a ordem de integração. ∫ 0 4 ∫ x 2 1 y 3 + 1d yd x
Esboce a região de integração e mude a ordem de integração. ∫ 0 4 ∫ 0 x f x , yd yd x
Calcule a integral trocando a ordem de integração.49. ∫ 0 1 ∫ a r c s e ny π / 2 cos x1 + cos 2 xd xd y
Inverta a ordem de integração.