Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
Seja a região de acima do gráfico de e abaixo da reta .
a) Escreva a integral dupla
como uma integral iterada.
b) Encontre uma integral iterada equivalente à integral encontrada no item (a) com a ordem de integração invertida.
c) Calcule uma das integrais iteradas encotradas nos itens (a) e (b).
Passo 1
a) Cara, escrever essa integral como uma integral iterada, é definir com extremos de integração e montar a integral de com eles.
A gente começa entendendo nossa região.
Ela é limitada pela curva , que é uma parábola virada para cima que passa pela origem. E , uma reta que passa pela origem e tem angulação de .
É uma boa ter o gráfico delas memorizado, tá? E aí esboçando nossa região , a região entre essas curvas, temos
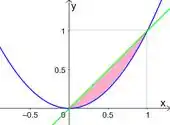
Repara que a interseção entre elas ocorre nos pontos e , beleza? Dá para achar isso calculando a interseção entre elas também:
Vamos ver como montar essa integral! Bora!
Passo 2
Vamos descrever como extremos de integração.
Precisamos limitar uma das variáveis entre constantes e a outra pode estar entre funções, beleza?
Vamos começar olhando para o eixo . A gente pode dizer que nele, a nossa região está limitada entre os valores de e .
Aí a gente diz:
Agora olhando para , a gente vê que ele (dentro do intervalo de que a gente definiu), está entre a reta , limitando nossa região por cima, e , limitando nossa região por baixo. Então a genta pode escrever:
Como está entre funções de , a gente diz que essa é uma região do tipo I.
Passo 3
Agora é montar a integral. Já temos o integrando:
Aí achamos os extremos de integração:
Aí como precisamos integrar primeiro em relação a variável que está entre funções, fica assim:
Prontinho! Tá aí nossa integral iterada.
Passo 4
b) Vamos descrever como extremos de integração de novo. Mas precisamos inverter a ordem de integração.
Para inverter a ordem de integração de uma integral dupla, a gente precisa colocar a variável que estava entre constantes entre funções, no nosso caso, colocar entre funções de .
E a variável que estava entre funções, colocamos entre constantes. No caso, colocar entre constantes.
Vamos começar olhando para o eixo . A gente pode dizer que nele, a nossa região está limitada entre os valores de e .
Aí a gente diz:
Agora, para limitar entre funções, precisamos achar nossas curvas como funções de . Basicamente é isolar nelas.
A nossa região está limitada pela esquerda por . Aí já está isolado. E estar limitada pela direita por . Isolando :
Vai ser a parte positiva da raiz, pois estamos na parte onde .
Aí a gente limita assim:
Como está entre constantes, a gente diz que essa é uma região do tipo II.
Passo 5
Agora é montar a integral. Já temos o integrando:
Aí achamos os extremos de integração:
Aí como precisamos integrar primeiro em relação a variável que está entre funções, fica assim:
Prontinho! Tá aí nossa integral iterada com a ordem de integração invertida.
Passo 6
c) Como a gente pode escolher, vamos calcular a integral do item (a), já que ela não tem nenhuma raiz, está mais fofa.
Fica assim:
Em relação a , vai ser constante, então podemos fazer:
Resposta
a)
b)
c)