Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
Provas antigas – Cálculo 2 – Unicamp – P2 6ª manhã – questão 1
Calcule a integral
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
Essa integral quando vemos parece ser simples de se feita, porém quando começamos a fazê-la percebemos que a técnica direta não é eficaz, e que as ordens de integração se embolam, e acaba sobrando um termo de para a integração do y. Sendo assim, a técnica mais eficiente é substituímos a ordem de integração, que é conforme veremos agora.
Para esse tipo de integração quando temos que inverter a ordem de integração, temos que fazer que fazer um gráfico das funções da ordem de integração. Para esse caso, é algo nessa pegada:
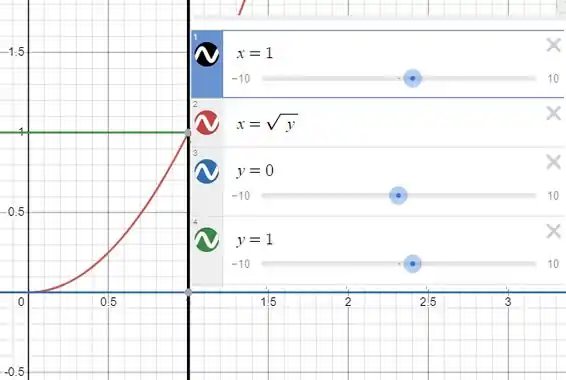
Onde as suas funções e suas core respectivas na tabela
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Sendo assim, nós temos a nossa integral com limites em termos de dx e dy, se queremos fazer em termos de dy dx teremos que tomar agora os limites com relação ao eixo x, assim vemos que:
Olhando a imagem do passo 1, vemos que x varia do centro ao ponto 1, ou seja de 0 até 1, assim:
Já y é uma questão mais complexa, e é dado pela função em vermelho, que é , assim e começa da origem também. Assim:
Resumindo, após a troca de intervalos temos:
Passo 3
Assim:
Integrando e y, temos:
Veja que temos dois termos com e para facilitar ainda mais, façamos uma substituição:
De forma que:
E quando fazemos uma substituição, qualquer que seja, devemos fazer uma analise de como que os novos limites d integração reagem à essa nova interação, sendo assim:
Integrando então em u:
Resumindo: