Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas

Ver Teoria
Exercício 84123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828385868788899091929394

Enunciado

Questão 1: Considere as regiões do plano

R 1 = x ,   y ∈ R 2   |     y ≤ 1 + x 2 ,

R 2 = x ,   y ∈ R 2   |     y ≥ 1

R 3 = x ,   y ∈ R 2   |     0 ≤ x ≤ 1 .

Seja R = R 1 ∩ R 2 ∩ R 3 . Seja S = x ,   y ∈ R 2   |     0 ≤ x ≤ 1 ,     0 ≤ y ≤ 1 .

  1. Esboce R hachurando. Esboce a fronteira de R .
  2. Escreva a integral dupla

    3. I = ∫     ∫ R   x y x 2 + y 2   d x d y

    Na forma de uma integral iterada integrando primeiro com respeito a y e em seguida com respeito a x .

  3. Escreva a integral dupla

    4. I = ∫     ∫ R   x y x 2 + y 2   d x d y

    Na forma de uma integral iterada integrando primeiro com respeito a x e em seguida com respeito a y .

  4. Seja

    5. J = I + ∫     ∫ S   x y ⋅ ln ⁡ x 2 + 1   d x d y

    Efetue a integração e escreva J na forma de uma integral simples

    J = ∫ a b f t d t ;

    Explicitando   a , b e f t .

    Obs.: Neste item não é necessário encontrar o valor numérico de J , apenas escrevê-la no formato pedido.

  5. Calcule J .

Passo 1

a )

Ok! Não há tempo a perder nessa prova, pois ela é um pouco grandinha, então vamos nessa?

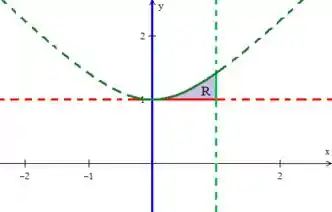
O primeiro item nos pede que desenhemos a região R . Como sabemos, ele é a intersecção de três regiões:

R 1 = x ,   y ∈ R 2   |     y ≤ 1 + x 2 ,

R 2 = x ,   y ∈ R 2   |     y ≥ 1

R 3 = x ,   y ∈ R 2   |     0 ≤ x ≤ 1 .

Veja que com essas três regiões, tiramos algumas igualdades muito interessantes pra gente:

1 º )             y = 1 + x 2

2 º )                                     y = 1

3 º )                                     x = 0

4 º )                                     x = 1

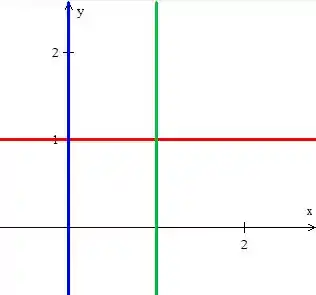
Então, basicamente o que temos que fazer aqui é desenhar o gráfico no X Y de todas essas igualdades. Vamos começar com as três últimas que é um pouco mais fácil, afinal todas elas nos representam retas...

Para a primeira curva, precisamos pensar um pouco mais, pois ela não tão “trivial” assim. Mas veja que elevando em ambos os lados ao quadrado e jogando x 2 pro outro lado...

y = 1 + x 2               →                     y 2 = 1 + x 2             →

y 2 - x 2 = 1

Veja que essa curva já é conhecida! Ela é uma hipérbole no plano x y ...

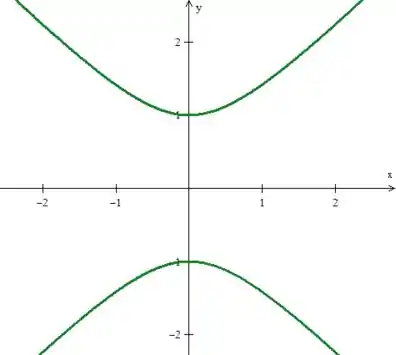
Veja então que a nossa região é a intercessão te todas essas curvas... Como queremos a parte onde y ≥ 1 , a região R está representada como sendo...

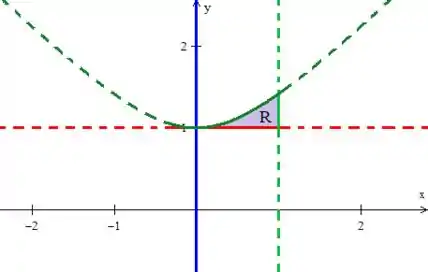
A fronteira de R então é:

Passo 2

b )

Agora vamos escrever a integral dupla abaixo com relação a y , na mais interior, e depois, na mais externa, em relação à x nessa ordem:

I = ∫     ∫ R   x y x 2 + y 2   d y d x

Sempre em integrais duplas, a variável que está variando por último deve variar entre intervalos numéricos reais. Como x é a variável mais externa, então ela vai assumir esse papel. Isso significa que devemos escrever a região R como do TIPO I:

Veja que nesse caso, x varia de 0 até 1 ...

0 ≤ x ≤ 1

Enquanto y varia da reta y = 1 até o “teto” que é a hipérbole...

1 ≤ y ≤ 1 + x 2

Então...

I = ∫ 0 1 ∫ 1 1 + x 2 x y x 2 + y 2   d y d x

Passo 3

c )

Agora vamos fazer o mesmo que fizemos no item anterior, mas dessa vez, vamos escrever na ordem...

I = ∫     ∫ R   x y x 2 + y 2   d x d y

Onde agora y quem vai variar entre intervalos numéricos. Ou seja, vamos descrever R agora como sendo uma região TIPO II:

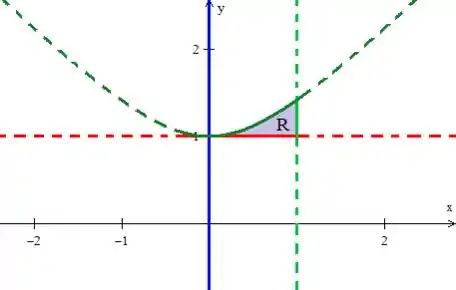
Mas veja que para isso, precisamos encontrar qual é o y m á x ( y máximo) de variação da região, já que o mínimo é dado pela base reta onde y = 1 ...

1 ≤ y ≤ y m á x

No desenho da nossa região, conseguimos identificar que o valor máximo que y assume é dado pelo ponto mais de cima definido pelo encontro da reta verde claro com a hipérbole em verde escuro. Esse ponto é facilmente encontrado pegando a reta x = 1 e substituindo na equação da hipérbole...

y = 1 + x 2             →             y = 1 + 1 2             →

y m á x = 2

Logo...

1 ≤ y ≤ 2

Ok! Mas ainda falta a variação de x e, ora... Se y ficou com o papel de x , o x deve ficar com o papel de y e variar entre curvas, ou seja, x deve variar entre duas paredes agora...

p a r d e   d i r e i t a ≤ x ≤ p a r e d e   e s q u e r d a

A parede direita é a hipérbole...

y 2 - x 2 = 1           →               x 2 = y 2 - 1         →

x = y 2 - 1

Enquanto a parede a esquerda é a reta x = 1 ...

y 2 - 1 ≤ x ≤ 1

Então...

I = ∫ 1 2 ∫ y 2 - 1 1 x y x 2 + y 2   d x d y

Passo 4

d )

O que vamos fazer agora é escrever essa integral aqui

J = I + ∫     ∫ S   x y ⋅ ln ⁡ x 2 + 1   d x d y

Para

J = ∫ a b f t d t

Essa integral dupla aí em S , pode ser facilmente descrita na sua forma iterada, já que...

S = x ,   y ∈ R 2   |     0 ≤ x ≤ 1 ,   0 ≤ y ≤ 1

∫ 0 1 ∫ 0 1 x y ⋅ ln ⁡ x 2 + 1   d y d x

Então...

J = ∫     ∫ R   x y x 2 + y 2   d x d y + ∫ 0 1 ∫ 0 1 x y ⋅ ln ⁡ x 2 + 1   d y d x         →

Perceba que podemos pegar qualquer uma das duas integrais iteradas que encontramos para I , mas é mais aconselhável à primeira:

J = ∫ 0 1 ∫ 1 1 + x 2 x y x 2 + y 2   d y d x + ∫ 0 1 ∫ 0 1 x y ⋅ ln ⁡ x 2 + 1   d y d x

Porque assim teremos duas integrais escritas nas mesmas ordens, enquanto os limites mais externos sendo os mesmos, o que facilita o nosso trabalho !

Passo 5

Podemos então agora calcular a integral de dentro de ambas! Vamos começar com a primeira...

∫ 0 1 ∫ 1 1 + x 2 x y x 2 + y 2   d y d x =

∫ 0 1 x ∫ 1 1 + x 2 y x 2 + y 2   d y d x

Fazendo uma substituição simples...

u = x 2 + y 2             →             d u = 2 y d y           o u           y d y = d u 2

Não se esqueça de trocar os limites também...

y = 1             →               u = x 2 + 1

y = 1 + x 2             →               u = x 2 + 1 + x 2 2 = 2 x 2 + 1

∫ 0 1 x ∫ 1 1 + x 2 y x 2 + y 2   d y d x = ∫ 0 1 x ∫ x 2 + 1 2 x 2 + 1 1 u   d u 2 d x =

∫ 0 1 x ln ⁡ u 2 x 2 + 1 2 x 2 + 1 d x = ∫ 0 1 x ln ⁡ 2 x 2 + 1 - ln ⁡ x 2 + 1 2 d x

Passo 6

Vamos então calcular agora a integral de dentro, mas da segunda integral dupla daquele J ...

∫ 0 1 ∫ 0 1 x y ⋅ ln ⁡ x 2 + 1   d y d x         →

∫ 0 1 x ln ⁡ x 2 + 1 ∫ 0 1 y d y d x =

∫ 0 1 x ln ⁡ x 2 + 1 y 2 2 0 1 d x =

∫ 0 1 x ln ⁡ x 2 + 1 2 d x

Passo 7

Então...

J = ∫ 0 1 ∫ 1 1 + x 2 x y x 2 + y 2   d y d x + ∫ 0 1 ∫ 0 1 x y ⋅ ln ⁡ x 2 + 1   d y d x     →

J = ∫ 0 1 x ln ⁡ 2 x 2 + 1 - ln ⁡ x 2 + 1 2 d x + ∫ 0 1 x ln ⁡ x 2 + 1 2 d x =

J = ∫ 0 1 x ln ⁡ 2 x 2 + 1 2 - x ln ⁡ x 2 + 1 2 + x ln ⁡ x 2 + 1 2 d x =

J = ∫ 0 1 x ln ⁡ 2 x 2 + 1 2 d x

Onde, por comparação, temos...

J = ∫ a b f t d t = ∫ 0 1 x ln ⁡ 2 x 2 + 1 2 d x

a = 0 , b = 1 e

f t = t ln ⁡ 2 t 2 + 1 2

Passo 8

e )

Finalmente, vamos encontrar o valor final de J ...

J = ∫ 0 1 x ln ⁡ 2 x 2 + 1 2 d x

Fazendo uma substituição simples...

2 x 2 + 1 = p           →             d p = 4 x   d x     →

x   d x = d p 4

E...

x = 0                       →                           p = 2 0 2 + 1 = 1

x = 1                       →                           p = 2 1 2 + 1 = 3

J = ∫ 0 1 x ln ⁡ 2 x 2 + 1 2 d x = ∫ 1 3 ln ⁡ p 2 ⋅ d p 4   =

1 8 ∫ 1 3 ln ⁡ p d p  

Bem, essa integral aí se resolve fazendo uma integração por partes, onde ln ⁡ p a gente deriva e o 1 que o multiplica a gente integra:

u = ln ⁡ p             →                     d u = 1 p d p

d v = 1 d p                     →                       v = p

∫     u   d v = u v - ∫     v   d u     →

∫     ln ⁡ p   d p = p ⋅ ln ⁡ p - ∫     p   1 p d p     →

∫     ln ⁡ p   d p = p ⋅ ln ⁡ p - ∫     d p     →

∫     ln ⁡ p   d p = p ⋅ ln ⁡ p - p

Logo...

1 8 ∫ 1 3 ln ⁡ p d p   = 1 8 p ⋅ ln ⁡ p - p 1 3 =

1 8 ∫ 1 3 ln ⁡ p d p   = 1 8 3 ⋅ ln ⁡ 3 - 3 - 1 ⋅ ln ⁡ 1 - 1 =

1 8 ∫ 1 3 ln ⁡ p d p   = 1 8 3 ⋅ ln ⁡ 3 - 3 - - 1 =

1 8 ∫ 1 3 ln ⁡ p d p   = 3 8 ln ⁡ 3 - 1 4

Resposta

a )

b )   ∫ 0 1 ∫ 1 1 + x 2 x y x 2 + y 2   d y d x

c )   ∫ 1 2 ∫ y 2 - 1 1 x y x 2 + y 2   d x d y

d )   a = 0 ;     b = 1     e     f t = t ln ⁡ 2 t 2 + 1 2

e )   3 8 ln ⁡ 3 - 1 4

Exercícios de Livros Relacionados

Esboce a região de integração e mude a ordem de integração. ∫ 0 1 ∫ a r c t gx π / 4 f x , yd yd x
Calcule a integral trocando a ordem de integração. ∫ 0 4 ∫ x 2 1 y 3 + 1d yd x
Esboce a região de integração e mude a ordem de integração. ∫ 0 4 ∫ 0 x f x , yd yd x
Calcule a integral trocando a ordem de integração.49. ∫ 0 1 ∫ a r c s e ny π / 2 cos ⁡ x1 + cos 2 ⁡ xd xd y
Inverta a ordem de integração.