Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas

Ver Teoria
Exercício 39123456789101112131415161718192021222324252627282930313233343536373840414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

IME, Cálculo 2, 2018, VE2, Q1

Inverta a ordem de integração da seguinte integral dupla:

∫ 0 1 ∫ x - x 2 2 x ( x + y ) d y d x

Passo 1

Faala, pessoal! O primeiro passo para inverter a ordem de uma integral dupla é montar o gráfico da região. Feito isso é possível estabelecer novos limites de integração. Assim sendo, temos:

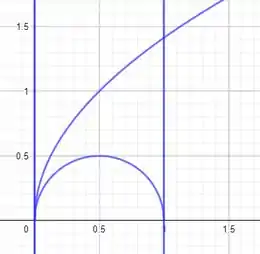
Observe que na prática podemos integrar a área à direita de 2 x e subtrair a integral dentro da curva x - x 2 . Na primeira, teremos: y 2 2 ≤ x ≤ 1 com 0 ≤ y ≤ 2   , pois:

y = 2 x ⇒ x = y 2 2

E o ponto de interseção entre x = 1 e y = 2 x ocorre em y = 2 . Quanto a segunda região, interna a y = x - x 2 , temos de escrever x em função de y :

y = x - x 2 ⇒ x 2 - x + y 2 = 0

⇒ x = 1 ± 1 - 4 y 2 2

Que nos gera duas curvas, uma para x ≤ 1 / 2 que será o limite inferior e outra para x ≥ 1 / 2 que será o limite superior. Assim, os limites de integração serão:

1 - 1 - 4 y 2 2 ≤ x ≤ 1 + 1 - 4 y 2 2                                       0 ≤ y ≤ 1 / 2

Onde o valor máximo de y = 1 / 2 se deve a 1 - 4 y 2 ≥ 0 . Assim, a ordem invertida fica:

∫ 0 1 ∫ x - x 2 2 x ( x + y ) d y d x = ∫ 0 2 ∫ y 2 / 2 1 ( x + y ) d x d y - ∫ 0 1 / 2 ∫ 1 - 1 - 4 y 2 2 1 + 1 - 4 y 2 2 ( x + y ) d x d y

Resposta

∫ 0 1 ∫ x - x 2 2 x ( x + y ) d y d x = ∫ 0 2 ∫ y 2 / 2 1 ( x + y ) d x d y - ∫ 0 1 / 2 ∫ 1 - 1 - 4 y 2 2 1 + 1 - 4 y 2 2 ( x + y ) d x d y

Exercícios de Livros Relacionados

Esboce a região de integração e mude a ordem de integração. ∫ 0 1 ∫ a r c t gx π / 4 f x , yd yd x
Calcule a integral trocando a ordem de integração. ∫ 0 4 ∫ x 2 1 y 3 + 1d yd x
Esboce a região de integração e mude a ordem de integração. ∫ 0 4 ∫ 0 x f x , yd yd x
Calcule a integral trocando a ordem de integração.49. ∫ 0 1 ∫ a r c s e ny π / 2 cos ⁡ x1 + cos 2 ⁡ xd xd y
Inverta a ordem de integração.