Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
Integrais duplas sobre regiões gerais
Calcule a integral
Passo 1
Deveríamos começar a questão pela integral de dentro, mas ela não parece muito simples em primeiro momento. Vamos, então, tentar mudar essa ordem de integração para ver se a integral fica mais fácil.
Primeiro, vamos esboçar a região em questão. Temos variando de a e entre e . Você não sabe desenhar a curva ? Faça assim: substitua e na equação e encontre os valores correspondentes de (teremos e ). Seu gráfico não precisa ficar perfeito, só precisamos saber que a região de integração tem essa cara:
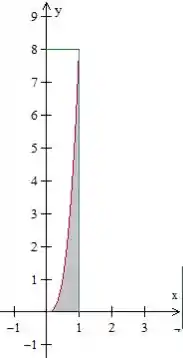
Passo 2
Agora vamos reescrever essa região como tipo I. Pelo próprio gráfico, vemos que varia entre e , portanto .
Já o valor de varia entre e a curva vermelha, vamos escrevê-la em função de (isolando o ):
Nossa região de integração será, então:
Passo 3
Podemos, então, reescrever a integral da seguinte forma:
Passo 4
Vamos, agora, integrar em relação a :
Passo 5
Veja como ficou mais simples integrar o termo dentro da raiz: se chamarmos
temos
Temos que acertar os limites de integração
e a integral passa a ser:
Integrando em relação a , temos: