Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas

Enunciado

Ok, não conseguimos integrar isso aí de cara, né? Pelo menos não em , mas em seria tranquilo, certo?

Vamos tentar trocar essa ordem de integração então para ver se fica mais fácil. Temos as seguintes equações:

Para entender o gráfico da primeira função, podemo pensar em , que nós sabemos que tem o seguinte formato:

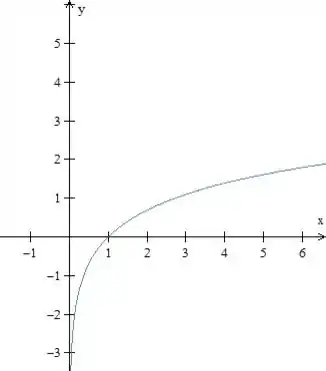
A função é essa aí “movida” para a esquerda. Repare que essa função corta a origem, pois . Temos o seguinte:

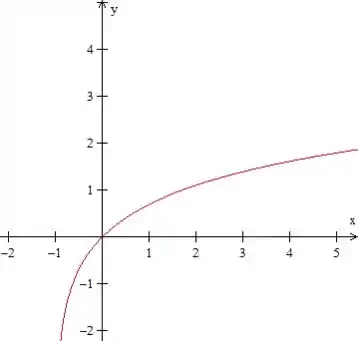
Certo, agora podemos fazer um esboço da nossa região de integração:

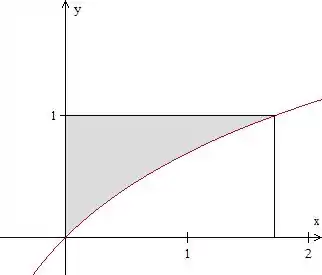
Repare que .

Pelo gráfico, vemos que varia entre a curva e e que varia entre e . Mas para escrever essa região como tipo II, precisamos isolar o em , não é?

Logo, temos variando desde até . Pronto, basta levar esses valores para a integral de forma invertida, teremos:

Você verá que essa troca facilitará muito nossa vida!

Vamos integrar, então, em relação a :

Agora integramos em relação a . Vamos fazer: