Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
Calcule a Integral Dupla
Passo 1
Resolver essa integral primeiro em relação a x, e depois aplicar aquele intervalo, com certeza fica muito difícil de resolver. Por isso, a primeira coisa que tem que vir na nossa cabeça é fazer uma mudança de ordem, certo? Bora lá então
O que isso conclui pra gente?
Isso nos mostra que a região é a metade direita de uma elipse, se liga na figura.
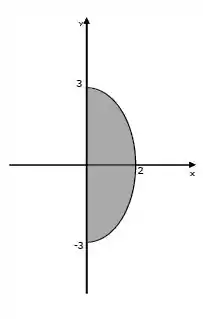
Passo 2
Vamos então transforma-la como uma do tipo 2 para uma do tipo 1, onde ao invés de x varias entre funções e y por constantes, x variará entre constantes, e y entre funções.
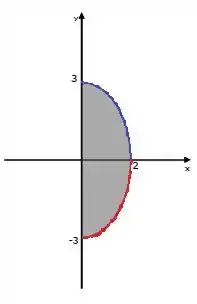
Escreveremos então que x vai variar entre 0 e 2, como pode ser observado na imagem acima, enquanto y variará entre a função vermelha e a azul, tudo bem?
Passo 3
Agora podemos então reescrever a integral e resolver
Resposta
Exercícios de Livros Relacionados
Esboce a região de integração e mude a ordem de integração. ∫ 0 1 ∫ a r c t gx π / 4 f x , yd yd x
Calcule a integral trocando a ordem de integração. ∫ 0 4 ∫ x 2 1 y 3 + 1d yd x
Esboce a região de integração e mude a ordem de integração. ∫ 0 4 ∫ 0 x f x , yd yd x
Calcule a integral trocando a ordem de integração.49. ∫ 0 1 ∫ a r c s e ny π / 2 cos x1 + cos 2 xd xd y
Inverta a ordem de integração.