Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
Origem do Exercício
Inverta a ordem da integral, esboce a região de integração se achar necessário e calcule a integral:
Passo 1
Essa função é bastante difícil de integrar, mas se dermos sorte, quando invertermos a ordem de integração, vai acontecer alguma coisa para simplificar nossa vida!
O primeiro passo é identificar a região em que estamos integrando, para depois reescrevermos ela de outra forma.
Na região atual, o está variando entre e , e para cada um desses valores de , o varia entre a função e :
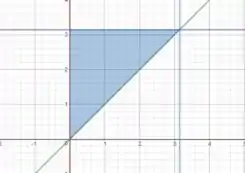
Então nossa tarefa é: reescrever essa região.
Passo 2
Antes, nós tínhamos limitado o por constantes:
E o tem uma função em um dos limites:
Agora vamos inverter isso, vamos limitar por constantes. Olhando para a imagem, dá pra ver que todos os pontos na região azul tem coordenada nesse intervalo:
Em seguida fazemos a seguinte pergunta: para cada valor de nesse intervalo, como varia o ? A resposta está na imagem! O vai sempre do até a função
Então nossa integral fica assim:
Passo 3
Agora já estamos prontos para resolver a integral, vamos ver se a inversão de ordem resolveu alguma coisa:
Começamos integrando em relação a . Nesse caso, podemos pensar em como uma constante e colocar toda aquela função para “fora” da integral:
Resolvendo a integral da direita:
Então:
Agora sim podemos resolver! A integral do é , ou seja:
Resposta
O valor da integral é .