Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
UFU, Sem Campus, Cálculo 2, Listas de C2 - Profª Ana Paula - Lista 7 - Integrais Duplas, Questão 7b
Esboce a região de integração e faça a mudança de ordem de integração.
b)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para esboçar a região de integração e faça a mudança de ordem de integração da seguinte integral dupla:
Bom.. analisando a integral, vemos que a região de integração está entre a curva e a reta , delimitada no intervalo :
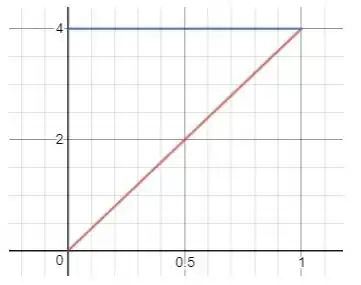
Agora devemos mudar a ordem de integração e reescrever a integral!!
Eaí? Bora lá?
😉
Passo 2
Bom... mudando a ordem de integração, vemos que varia de (eixo ) a .
Enquanto isso, varia de a .
Assim, temos:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Esboce a região de integração e mude a ordem de integração. ∫ 0 1 ∫ a r c t gx π / 4 f x , yd yd x
Calcule a integral trocando a ordem de integração. ∫ 0 4 ∫ x 2 1 y 3 + 1d yd x
Esboce a região de integração e mude a ordem de integração. ∫ 0 4 ∫ 0 x f x , yd yd x
Calcule a integral trocando a ordem de integração.49. ∫ 0 1 ∫ a r c s e ny π / 2 cos x1 + cos 2 xd xd y
Inverta a ordem de integração.