Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
Unicamp, Cálculo 2, 2019.2, P2, Questão 1.
Resolva a integral
Passo 1
Uma boa forma de começar qualquer questão de integral dupla é fazendo um esboço da região em que a gente está integrando.
Os limites de integração são esses aqui:
Então no eixo , a gente está abaixo da reta e acima de :
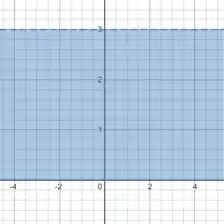
Vamos dar uma olhada na condição :
Talvez fique mais fácil entender de outro jeito:
Ou seja, estamos sempre abaixo da reta , e à esquerda da reta vertical . Juntando todas essas condições, a gente chega nessa região aqui:
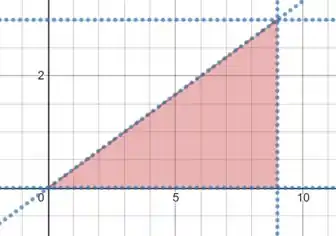
Passo 2
Então tá, agora com esse gráfico talvez fique mais fácil entender o problema:
Não dá pra resolver essa integral do jeito que está. Vamos tentar inverter a ordem de integração para tentar melhorar a situação.
No momento os intervalos de integração são esses:
A gente quer trocar essa ordem, então vamos limitar por constantes, ao invés de .
Olhando o desenho: entre quais valores fixos o varia?
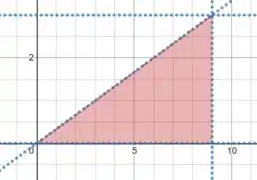
E para a coordenada ? O valor mínimo é zero:
E o valor máximo é aquela reta que vimos antes:
Então os novos limites de integração são:
E a nossa integral fica:
Agora vamos tentar resolver.
Passo 3
O primeiro passo é resolver a integral de dentro, então:
Nesse caso, como estamos integrando em relação a , a função funciona como constante:
E colocando isso na integral, ficamos com:
Beleza, agora a integral pode ser resolvida.
Passo 4
Agora ficamos com o seguinte:
Essa integral a gente já conhece, dá pra resolver com uma substituição:
E temos que mudar também os limites de integração:
Substituindo isso na integral:
Agora vamos cortar aquele de dentro da integral, e aí ficamos com a integral de uma exponencial
A integral de é , então:
Pronto! Resolvemos a integral!
Resposta
A integral é .