Calcule a seguinte integral iterada
Passo 1
Vamos começar então entendendo o nosso problema.
Observe que a integral acima não é tão trivial de se resolver na ordem que ela está. Qual é a dica?! Simmmm!!! Mudança da ordem de integração! :) Vamos ver como isso vai ficar?
Passo 2
Primeiro, vamos mudar a configuração da nossa região e para fazer isso, vamos olhar para o seu gráfico no plano cartesiano.
Repare que
Se desenharmos no nosso gráfico essas quatro curvas: , , , e ; vamos encontrar nossa região dentro de todas elas.
Então bora desenhar a primeira! é equivalente ao ramo onde é positivo da parábola
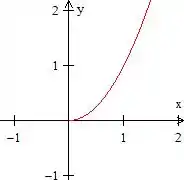
Quanto as retas:
- e , são retas paralelas ao eixo e que passam por esse valor de (inclusive coincide com o próprio eixo , se lembra?)
- De modo análogo, é uma reta paralela a e passa por
Juntando tudo, encontraremos nossa região
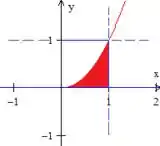
Passo 3
Vamos agora mudar a configuração da nossa região.
Antes ela estava configurada como uma região do tipo 2, agora vamos configurá-la como uma região do tipo 1, ou seja
- varia em um intervalo numérico bem definido
- varia da reta até a parábola
Passo 4
Agora é só montar a integral e correr para o abraço! :)
Note como ficou mais fácil!
Bem... resolvendo primeiro a integral de dentro lembrando que se vamos integrar em a gente deve tomar como constante...
Substituindo os limites de ...
Agora podemos fazer uma substituição
Não esqueça de mudar os limites!