Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
Calcule:
Com
Passo 1
A questão é bem direta, né? Só precisamos calcular a integral que ele nos deu, só que integrar esse cara aí em relação a parece ser bem complicado! Para tentar facilitar isso, vamos inverter a ordem de integração, lembra como faz isso? Primeiro vamos desenhar o gráfico dos limites:
Temos as seguintes equações nos limites de :
Essas funções variando no intervalo de , fazendo o esboço do gráfico temos:
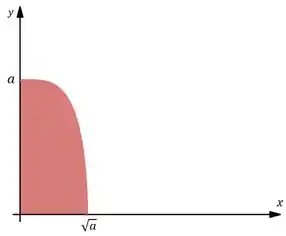
Onde estamos interessados na região vermelha.
Passo 2
Agora vamos encontrar os novos limites!
Vamos isolar na nossa equação pra ver qual vai ser o seu limite:
Veja que a gente achou um limite bem parecido com a função que precisamos integrar!! Da pra imaginar que estamos no caminho certo!
Portanto vemos que nossos novos limites são
Passo 3
Vamos reescrever então a nossa função:
Passo 4
Integrar isso em é simples né? Só de mudar os limites de integração já facilitou muito nossas contas! Como não temos nenhum termo dentro da integral vamos ficar com isso aqui:
Passo 5
Integrando em :