Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas

Ver Teoria
Exercício 56123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

Calcule a integral

∫ 1 5 ∫ x 5 y x ln ⁡ y   d y d x

Passo 1

Bom, questão diretona ao ponto. Bora sempre começar dando uma olhada na região.

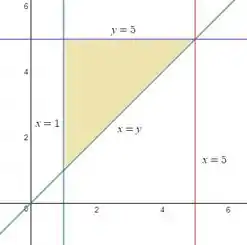
Vamos então aplicar Fubini.

∫ 1 5 ∫ x 5 y x ln ⁡ y   d y d x

Caraca, integral de y ln ⁡ y ...pesado. Isso nos leva a quê? Parabéns se você pensou em mudança de ordem!

Como que a gente fica então, observando no gráfico?

∫ 1 5 ∫ x 5 y x ln ⁡ y   d y d x = ∫ 1 5 ∫ 1 y y x ln ⁡ y d x d y

Agora é só resolver e ganhar esse pontinho na carteira.

Passo 2

Bora lá

∫ 1 5 ∫ 1 y y x ln ⁡ y d x d y

∫ 1 5 y ln ⁡ y   ln ⁡ x 1 y d y    

∫ 1 5 y ln ⁡ y   ln ⁡ y - ln ⁡ 1 d y  

Aquela facilitada aqui, uma vez que l n 1 = 0 .

∫ 1 5 y   d y

= 12

Sucesso demais!!

Resposta

12

Exercícios de Livros Relacionados

Esboce a região de integração e mude a ordem de integração. ∫ 0 1 ∫ a r c t gx π / 4 f x , yd yd x
Calcule a integral trocando a ordem de integração. ∫ 0 4 ∫ x 2 1 y 3 + 1d yd x
Esboce a região de integração e mude a ordem de integração. ∫ 0 4 ∫ 0 x f x , yd yd x
Calcule a integral trocando a ordem de integração.49. ∫ 0 1 ∫ a r c s e ny π / 2 cos ⁡ x1 + cos 2 ⁡ xd xd y
Inverta a ordem de integração.